题目内容
点A、B分别是椭圆C:
+
=1(a>b>0)长轴的左、右端点,点F是椭圆的右焦点,点P(
,
)在椭圆上,又椭圆离心率e=
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设M是椭圆长轴AB上的一点,M到直线AP的距离等于|MB|,求椭圆上的点到点M的距离d的最小值.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
| 3 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设M是椭圆长轴AB上的一点,M到直线AP的距离等于|MB|,求椭圆上的点到点M的距离d的最小值.
考点:椭圆的标准方程,点到直线的距离公式
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)依题意得
,由此能求出椭圆C的方程.
(Ⅱ)由(Ⅰ)知A(-6,0),B(6,0),直线AP的方程为x-
y+6=0,设点M(m,0),由题意得
=|m-6|,由此能求出当x=
时,d取得最小值.
|
(Ⅱ)由(Ⅰ)知A(-6,0),B(6,0),直线AP的方程为x-
| 3 |
| |m+6| |
| 2 |
| 9 |
| 2 |
解答:
解:(Ⅰ)依题意得
,
解得a2=36,b2=20,
∴椭圆C的方程为
+
=1.
(Ⅱ)由(Ⅰ)知A(-6,0),B(6,0),
∴直线AP的方程为x-
y+6=0,
设点M(m,0),由题意得
=|m-6|,
又-6≤m≤6,
∴m=2,∴d2=(x-2)2+y2=x2-4x+4+20-
x2=
(x-
)2+15,
∴当x=
时,d取得最小值
.
|
解得a2=36,b2=20,
∴椭圆C的方程为
| x2 |
| 36 |
| y2 |
| 20 |
(Ⅱ)由(Ⅰ)知A(-6,0),B(6,0),
∴直线AP的方程为x-
| 3 |
设点M(m,0),由题意得
| |m+6| |
| 2 |
又-6≤m≤6,
∴m=2,∴d2=(x-2)2+y2=x2-4x+4+20-
| 5 |
| 9 |
| 4 |
| 9 |
| 9 |
| 2 |
∴当x=
| 9 |
| 2 |
| 15 |
点评:本题考查椭圆方程的求法,考查椭圆上的点到点M的距离d的最小值的求法,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
相关题目
已知定义在[1,+∞)上的函数f(x)=
则下列结论正确的是( )
|
| A、函数f(x)的值域为[1,4] | ||
B、关于x的方程f(x)-
| ||
| C、当x∈[2n-1,2n](n∈N*)时,函数f(x)的图象与x轴围成的面积为3 | ||
| D、不存在实数x0,使不等式x0f(x0)>6成立 |
已知函数f(x)=(2x-1)2+ax2,若不等式f(x)<0的解集中恰有3个整数解,则( )
| A、f(1)f(2)<0 |
| B、f(2)f(3)<0 |
| C、f(3)f(4)<0 |
| D、f(4)f(5)<0 |
斜率为1的直线l经过抛物线y2=2x的焦点,且与抛物线相交于A、B两点,则线段AB的长是( )
A、2
| ||
| B、2 | ||
C、4
| ||
| D、4 |
角α(0<α<2π)的正、余弦线的长度相等,且正、余弦符号相异.那么α的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
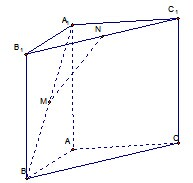 如图,直三棱柱ABC-A1B1C1,∠BAC=90°,AB=AC=
如图,直三棱柱ABC-A1B1C1,∠BAC=90°,AB=AC=