题目内容
5.已知函数$f(x)={x^2}+lg(x+\sqrt{{x^2}+1})$,若f(a)=M,则f(-a)等于( )| A. | 2a2-M | B. | M-2a2 | C. | 2M-a2 | D. | a2-2M |
分析 根据已知中函数$f(x)={x^2}+lg(x+\sqrt{{x^2}+1})$,f(a)=M,代入计算可得f(-a)的值.
解答 解:∵$f(x)={x^2}+lg(x+\sqrt{{x^2}+1})$,
∴f(a)=M=${a}^{2}+lg(a+\sqrt{{a}^{2}+1})$,
f(-a)=${a}^{2}+lg(-a+\sqrt{{a}^{2}+1})$,
f(a)+f(-a)=2a2,
故f(-a)=2a2-M,
故选:A
点评 本题考查的知识点是函数求值,对数运算,难度不大,属于基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
15.设集合A={x|x2-9<0},B={x|2x∈N},则A∩B的元素的个数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
16.已知全集U=R,集合A={x|x2-2x≤0},B={x|y=lg(x-1)},则集合A∩(∁UB)=( )
| A. | {x|x<0,或x>2} | B. | {x|0<x<2} | C. | {x|0≤x<1} | D. | {x|0≤x≤1} |
17.如图所示,在△ABC中,M在BC上,N在AM上,CM=CN,且$\frac{AM}{AN}$=$\frac{BM}{CN}$,下列结论中正确的是( )
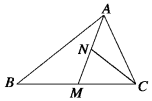

| A. | △ABM∽△ACB | B. | △ANC∽△AMB | C. | △ANC∽△ACM | D. | △CMN∽△BCA |