题目内容
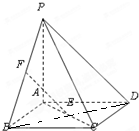
 如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点.
如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点.(Ⅰ)求证:EF∥平面PCD;
(Ⅱ)若PA=AB,求异面直线EF与PA所成角的大小.
考点:异面直线及其所成的角,直线与平面平行的判定
专题:计算题,作图题,空间位置关系与距离
分析:(1)连结BD,交AC于点E,可证EF∥PD,从而证明EF∥平面PCD.
(2)异面直线EF与PA所成角的平面角为∠APD,求其大小即可.
(2)异面直线EF与PA所成角的平面角为∠APD,求其大小即可.
解答:
 解:(1)证明:连结BD,交AC于点E,
解:(1)证明:连结BD,交AC于点E,
∵E,F分别是AC,PB的中点,
∴EF∥PD,又∵EF?平面PCD,PD?平面PCD;
∴EF∥平面PCD.
(2)由(1)知,异面直线EF与PA所成角的平面角为∠APD;
又∵PA=AB,∴PA=AD,
又∵PA⊥底面ABCD,∴△APD为等腰直角三角形,
∴∠APD=45°.
即异面直线EF与PA所成角为45°.
 解:(1)证明:连结BD,交AC于点E,
解:(1)证明:连结BD,交AC于点E,∵E,F分别是AC,PB的中点,
∴EF∥PD,又∵EF?平面PCD,PD?平面PCD;
∴EF∥平面PCD.
(2)由(1)知,异面直线EF与PA所成角的平面角为∠APD;
又∵PA=AB,∴PA=AD,
又∵PA⊥底面ABCD,∴△APD为等腰直角三角形,
∴∠APD=45°.
即异面直线EF与PA所成角为45°.
点评:本题考查了学生的空间想象力及线面平行的判定定理,属于基础题.

练习册系列答案
相关题目
下列现象是随机事件的是( )
| A、天上无云下大雨 |
| B、同性电荷,相互排斥 |
| C、没有水分,种子发芽 |
| D、从分别标有1,2,3,4,5,6,7,8,9,10的10张号签中任取一张,得到1号签 |
若函数f(x)对任意a>0且a≠1,都有f(ax)=af(x),则称函数为“穿透”函数,则下列函数中,不是“穿透”函数的是( )
| A、f(x)=-x |
| B、f(x)=x+1 |
| C、f(x)=|x| |
| D、f(x)=x-|x| |
各棱长均为a的三棱锥的表面积为( )
A、4
| ||
B、3
| ||
C、2
| ||
D、
|