题目内容
已知函数f(x)＝|x－3|，g(x)＝－|x＋4|＋m.
(1)已知常数a<2，解关于x的不等式f(x)＋a－2>0；
(2)若函数f(x)的图象恒在函数g(x)图象的上方，求实数m的取值范围．
[解析] (1)由f(x)＋a－2>0得|x－3|>2－a，
∴x－3>2－a或x－3<a－2，∴x>5－a或x<a＋1.
故不等式的解集为(－∞，a＋1)∪(5－a，＋∞)
(2)∵函数f(x)的图象恒在函数g(x)图象的上方，
∴f(x)>g(x)恒成立，即m<|x－3|＋|x＋4|恒成立．
∵|x－3|＋|x＋4|≥|(x－3)－(x－4)|＝7，
∴m的取值范围为m<7.
练习册系列答案
名校课堂系列答案
相关题目
，PC＝1，则圆O的半径等于________．
(θ为参数)，以原点为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为ρsinθ＋ρcosθ＝1，则直线l被圆C所截得的弦长是________．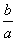
＋
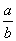≥2成立的条件有( )
(a∈R，i是复数单位)是纯虚数，则实数a＝________.