题目内容
2.已知等比数列{an}的通项公式为an=3en,请化简:lna1+lna2+…+lnan.分析 由已知中数列{an}为等比数列,且an>0,根据等比数列的性质,可得答案.
解答 解:若数列{an}为等比数列,且an=3en,则a1=3e,q=e
∴lna1+lna2+…+lnan=ln(a1•a2•…•an)=ln(3e•${e}^{\frac{n-1}{2}}$)n=n($\frac{n+1}{2}$+ln3)
点评 本题考查的知识点是等比数列的性质,对数的运算性质,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.在梯形ABCD中,AB∥CD,$\overrightarrow{AB}$=2$\overrightarrow{DC}$,$\overrightarrow{BE}$=$\overrightarrow{EC}$,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则向量$\overrightarrow{AE}$等于( )
| A. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | B. | $\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | C. | $\frac{3}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$ | D. | $\frac{2}{3}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ |
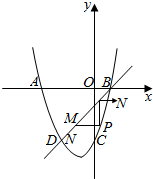 如图,抛物线y=ax2+2x-6与X轴交于点A(-6,0),B(点A在点B的左侧),与y轴交于点C,直线BD与抛物线交于点D,点D与点C关于该抛物线的对称轴对称.
如图,抛物线y=ax2+2x-6与X轴交于点A(-6,0),B(点A在点B的左侧),与y轴交于点C,直线BD与抛物线交于点D,点D与点C关于该抛物线的对称轴对称.