题目内容
3.函数y=lg(3-x)(2x-1)的定义域为(0,3).分析 根据函数y的解析式,列出不等式(3-x)(2x-1)>0,求出解集即可.
解答 解:∵函数y=lg(3-x)(2x-1),
∴(3-x)(2x-1)>0,
即$\left\{\begin{array}{l}{3-x>0}\\{{2}^{x}-1>0}\end{array}\right.$,或$\left\{\begin{array}{l}{3-x<0}\\{{2}^{x}-1<0}\end{array}\right.$;
解得0<x<3,
∴函数y的定义域为(0,3).
故答案为:(0,3).
点评 本题考查了根据对数函数的解析式求定义域的应用问题,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.定义在R的奇函数f(x),当x<0时,f(x)=-x2+x,则f(2)等于( )
| A. | 4 | B. | 6 | C. | -4 | D. | -6 |
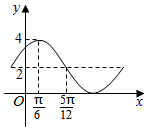 已知函数f(x)=Asin(ωx+φ)+B(A>0,ω,0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)的值为3.
已知函数f(x)=Asin(ωx+φ)+B(A>0,ω,0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)的值为3.