题目内容
下列积分中①
dx;②
-2xdx;③∫
dx;④
dx,积分值等于1的个数是( )
| ∫ | e 1 |
| 1 |
| x |
| ∫ | 2 -2 |
2 0 |
| ||
| π |
| ∫ |
0 |
| cos2x |
| cosx-sinx |
| A、1 | B、2 | C、3 | D、4 |
考点:定积分
专题:导数的综合应用
分析:根据积分公式分别进行计算即可判断.
解答:
解:①
dx=lnx|
=lne-ln1=1,满足条件;
②
-2xdx=(-x2)|
=-(4-4)=0,不满足条件;
③∫
dx的几何意义为x2+y2=4对应圆的面积
的
倍,即
×
×π×22=1,满足条件;
④
dx=
dx=
(cosx+sinx)dx=(sinx-cosx)|
=sin
-cos
-sin0+cos0=1+1=2,不满足条件.
故只有①③满足条件.
故选:B.
| ∫ | e 1 |
| 1 |
| x |
e 1 |
②
| ∫ | 2 -2 |
2 -2 |
③∫
2 0 |
| ||
| π |
| 1 |
| 4 |
| 1 |
| π |
| 1 |
| π |
| 1 |
| 4 |
④
| ∫ |
0 |
| cos2x |
| cosx-sinx |
| ∫ |
0 |
| cos2x-sin2x |
| cosx-sinx |
| ∫ |
0 |
0 |
| π |
| 2 |
| π |
| 2 |
故只有①③满足条件.
故选:B.
点评:本题主要考查积分的计算,要求熟练掌握常见函数的积分公式.

练习册系列答案
相关题目
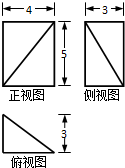
若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于( )

| A、10cm3 |
| B、20cm3 |
| C、30cm3 |
| D、40cm3 |
一个几何体的三视图如图所示,其中俯视图是一个菱形,则该几何体的体积为( )


A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数y=
的图象大致为( )
| ex+e-x |
| ex-e-x |
A、 |
B、 |
C、 |
D、 |