题目内容
在区间(1,2)内随机取个实数a,则直线y=2x,直线x=a与x轴围成的面积大于
的概率是( )
| 9 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:求出直线y=2x,直线x=a与x轴围成的面积大于
的等价条件,利用几何概型的概率公式即可得到结论.
| 9 |
| 4 |
解答:
 解:当x=a时,y=2a,即A(a,2a),B(a,0),
解:当x=a时,y=2a,即A(a,2a),B(a,0),
则△ABO的面积S=
×a•2a=a2,
若直线y=2x,直线x=a与x轴围成的面积大于
,
即a2>
,解得a>
,
∵1<a<2,∴
<a<2,
则对应的概率P=
=
,
故选:B
 解:当x=a时,y=2a,即A(a,2a),B(a,0),
解:当x=a时,y=2a,即A(a,2a),B(a,0),则△ABO的面积S=
| 1 |
| 2 |
若直线y=2x,直线x=a与x轴围成的面积大于
| 9 |
| 4 |
即a2>
| 9 |
| 4 |
| 3 |
| 2 |
∵1<a<2,∴
| 3 |
| 2 |
则对应的概率P=
2-
| ||
| 2-1 |
| 1 |
| 2 |
故选:B
点评:本题主要考查几何概型的概率的计算,根据条件求出a的取值范围是解决本题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
已知x>0,y>0,若不等式
≥
恒成立,则实数k的最大值为( )
| x+2y |
| xy |
| k |
| 2x+y |
| A、9 | B、10 | C、8 | D、7 |
执行如图所示的程序框图,输出的S值为( )


| A、-6 | B、-10 | C、6 | D、10 |
已知f(x)是R上的奇函数,且满足f(x+2)=-f(x),当x∈(0,2)时,f(x)=2x2+3,则f(7)=( )
| A、-5 | B、5 |
| C、-101 | D、101 |
已知a+2i=1+2bi(a,b∈R),其中i为虚数单位,则a+b=( )
| A、2 | B、-2 | C、1 | D、-1 |
等边△ABC的边长为2,D为AB的中点,E为线段AC上一动点,则
•
的取值范围是( )
| EB |
| ED |
| A、[2,9] | ||
B、[
| ||
C、[
| ||
D、[
|
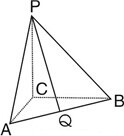 如图,三棱锥P-ABC中,PC,AC,BC两两互相垂直,AC=2,BC=4,PC=3,Q为AB中点,则线段PQ的长是( )
如图,三棱锥P-ABC中,PC,AC,BC两两互相垂直,AC=2,BC=4,PC=3,Q为AB中点,则线段PQ的长是( )A、
| ||
B、
| ||
C、
| ||
D、2
|
若x=-1是函数f(x)=ax3-3x的一个极值点,则a的值为( )
| A、-1 | B、-2 | C、1 | D、2 |