题目内容
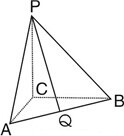如图，三棱锥P-ABC中，PC，AC，BC两两互相垂直，AC=2，BC=4，PC=3，Q为AB中点，则线段PQ的长是（ ）A、
| ||
B、
| ||
C、
| ||
D、2
|
考点：棱锥的结构特征
专题：空间位置关系与距离
分析：根据题意，PC，AC，BC两两互相垂直，可以建立空间直角坐标系，利用两点间的距离求出线段PQ的长．
解答：
解：建立如图所示的空间直角坐标系C-xyz，
∴A（0，2，0），B（4，0，0），P（0，0，3），
则AB的中点Q（2，1，0）；
∴|PQ|=
=
．
故选：C．
解：建立如图所示的空间直角坐标系C-xyz，∴A（0，2，0），B（4，0，0），P（0，0，3），
则AB的中点Q（2，1，0）；
∴|PQ|=
| (2-0)2+(1-0)2+(0-3)2 |
| 14 |
故选：C．
点评：本题考查了求空间中两点间距离的问题，解题时可以根据垂直关系，建立空间直角坐标系，求出两点间的距离，是基础题．
练习册系列答案
快乐5加2金卷系列答案
相关题目
从1，2，3，4这四个数中一次随机地取两个数，则其中一个数是另一个的两倍的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
在区间（1，2）内随机取个实数a，则直线y=2x，直线x=a与x轴围成的面积大于
的概率是（ ）
| 9 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知f（x）是定义在（-∞，+∞）上的偶函数，且在（-∞，0]上是增函数，设a=f（log47），b=f（log
3），c=f（21.6），则a，b，c的大小关系是（ ）
| 1 |
| 2 |
| A、c＜a＜b |
| B、c＜b＜a |
| C、b＜c＜a |
| D、a＜b＜c |
运行如图的程序框图，输出S的值为（ ）
| A、0 | ||||
B、
| ||||
C、
| ||||
D、-
|
已知集合A={-1，0，1，2}，B={0，2，3}，则A∩B等于（ ）
| A、{0，1，2} |
| B、{0，2，3} |
| C、{0，2} |
| D、{-1，0，1，2，3} |
已知全集U=R，若函数f（x）=x2-3x+2，集合M={x|f（x）≤0}，N={x|f′（x）＜0}，则M∩∁UN=（ ）
A、[
| ||
B、[
| ||
C、（
| ||
D、（
|
曲线y=
在点M（
，0）处的切线斜率为（ ）
| sinx |
| sinx+cosx |
| π |
| 4 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|