题目内容
12.函数f(x)=sin(ln$\frac{x-1}{x+1}$)的图象大致为( )| A. |  | B. |  | ||
| C. |  | D. |  |
分析 利用函数的定义域以及函数的奇偶性,特殊值的位置,排除选项判断即可.
解答 解:函数f(x)=sin(ln$\frac{x-1}{x+1}$)的定义域为:x>1或x<-1,排除A,
f(-x)=sin(ln$\frac{-x-1}{-x+1}$)=sin(-ln$\frac{x-1}{x+1}$)=-sin(ln$\frac{x-1}{x+1}$)=-f(x),函数是奇函数排除C,
x=2时,函数f(x)=sin(ln$\frac{1}{3}$)=-sin(ln3)<0,对应点在第四象限,排除D.
故选:B.
点评 本题考查函数的奇偶性以及定义域特殊点的应用,函数的图象的判断,考查计算能力.

练习册系列答案
相关题目
2.若圆锥曲线C:x2+my2=1的离心率为2,则m=( )
| A. | $-\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
3.将函数y=sin(x+$\frac{π}{6}$)的图象上所有的点向左平移$\frac{π}{4}$个的单位长度,再把图象上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得图象的解析式为( )
| A. | y=sin(2x+$\frac{5π}{12}$) | B. | y=sin($\frac{x}{2}$+$\frac{5π}{12}$) | C. | y=sin ($\frac{x}{2}$-$\frac{π}{12}$) | D. | y=sin($\frac{x}{2}$+$\frac{5π}{24}$) |
4.若复数z满足z(4-i)=5+3i(i为虚数单位),则$\overline z$为( )
| A. | 1-i | B. | -1+i | C. | 1+i | D. | -1-i |
1.已知点P在直线x=-1上移动,过点P作圆(x-2)2+(y-2)2=1的切线,相切于点Q,则切线长|PQ|的最小值为( )
| A. | 2 | B. | $2\sqrt{2}$ | C. | 3 | D. | $\sqrt{10}$ |
2.若实数x,y满足约束条件$\left\{\begin{array}{l}{x≤1}\\{y≤2}\\{2x+y≥2}\end{array}$,则z=x2+y2的最小值是( )
| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{4}{5}$ | C. | 1 | D. | 4 |
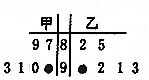 在学校组织的“环保知识”竞赛活动中,甲、乙两班6名参赛选手的成绩的茎叶图受到不同程度的污损,如图:
在学校组织的“环保知识”竞赛活动中,甲、乙两班6名参赛选手的成绩的茎叶图受到不同程度的污损,如图: