题目内容
20.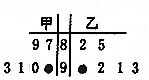 在学校组织的“环保知识”竞赛活动中,甲、乙两班6名参赛选手的成绩的茎叶图受到不同程度的污损,如图:
在学校组织的“环保知识”竞赛活动中,甲、乙两班6名参赛选手的成绩的茎叶图受到不同程度的污损,如图:(Ⅰ)求乙班总分超过甲班的概率;
(Ⅱ)若甲班污损的学生成绩是90分,乙班污损的学生成绩为97分,现从甲乙两班所有选手成绩中各随机抽取2个,记抽取到成绩高于90分的选手的总人数为ξ,求ξ的分布列及数学成绩.
分析 (Ⅰ)甲班前5位选手的总分为450,乙班前5位选手的总分为443,若乙班总分超过甲班,则甲、乙两班第六位选手的成绩可分别为:(90,98),(90,99),(91,99)三种情况,即可得出乙班总分超过甲班的概率.
(II)(Ⅱ)ξ的可能取值为0,1,2,3,4,利用相互独立与互斥事件的概率计算公式,进而得出分布列与数学期望.
解答 解:(Ⅰ)甲班前5位选手的总分为:87+89+90+91+93=450,
乙班前5位选手的总分为:82+85+92+91+93=443,
若乙班总分超过甲班,则甲、乙两班第六位选手的成绩可分别为:
(90,98),(90,99),(91,99)三种情况,
∴乙班总分超过甲班的概率P=$\frac{3}{10×10}$=$\frac{3}{100}$.
(Ⅱ)ξ的可能取值为0,1,2,3,4,
P(ξ=0)=$\frac{{∁}_{4}^{2}{∁}_{2}^{2}}{{∁}_{6}^{2}•{∁}_{6}^{2}}$=$\frac{6}{225}$,
P(ξ=1)=$\frac{{∁}_{2}^{1}•{∁}_{4}^{1}•{∁}_{2}^{2}+{∁}_{4}^{2}•{∁}_{4}^{1}•{∁}_{2}^{1}}{{∁}_{6}^{5}•{∁}_{6}^{5}}$=$\frac{56}{225}$,
P(ξ=2)=$\frac{{∁}_{2}^{1}{∁}_{4}^{1}{∁}_{4}^{1}{∁}_{2}^{1}+{∁}_{4}^{2}{∁}_{4}^{2}}{{∁}_{6}^{2}•{∁}_{6}^{2}}$=$\frac{101}{225}$,
P(ξ=3)=$\frac{{∁}_{2}^{2}{∁}_{4}^{1}{∁}_{2}^{1}+{∁}_{2}^{1}{∁}_{4}^{1}{∁}_{4}^{2}}{{∁}_{6}^{2}{∁}_{6}^{2}}$=$\frac{56}{225}$,
P(ξ=4)=$\frac{{∁}_{2}^{2}{∁}_{4}^{2}}{{∁}_{6}^{2}{∁}_{6}^{2}}$=$\frac{6}{225}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{6}{225}$ | $\frac{56}{225}$ | $\frac{101}{225}$ | $\frac{56}{225}$ | $\frac{6}{225}$ |
点评 本题考查了茎叶图的性质、相互独立与互斥事件的概率计算公式、随机变量的分布列及其数学期望,考查了推理能力与计算能力,属于中档题.

 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案| A. | f(x)=-sin2x | B. | f(x)的图象关于x=-$\frac{π}{3}$对称 | ||
| C. | f($\frac{7π}{3}$)=$\frac{1}{2}$ | D. | f(x)的图象关于($\frac{π}{12}$,0)对称 |
 如图1,以BD为直径的圆O经过A,C两点,延长DA,CB交于P点,如图2,将PAB沿线段AB折起,使P点在底面ABCD的射影恰为AD的中点Q,AB=BC=1,BD=2,线段PB,PC的中点为E,F.
如图1,以BD为直径的圆O经过A,C两点,延长DA,CB交于P点,如图2,将PAB沿线段AB折起,使P点在底面ABCD的射影恰为AD的中点Q,AB=BC=1,BD=2,线段PB,PC的中点为E,F.


