已知点P在直线x=-1上移动.过点P作圆(x-2)2+(y-2)2=1的切线.相切于点Q.则切线长|PQ|的最小值为( )A．2B．$2\sqrt{2}$C．3D．$\sqrt{10}$ 题目和参考答案——青夏教育精英家教网—

题目内容

1．已知点P在直线x=-1上移动，过点P作圆（x-2）²+（y-2）²=1的切线，相切于点Q，则切线长|PQ|的最小值为（　　）

A．

B．

$2\sqrt{2}$

C．

D．

$\sqrt{10}$

分析先求出圆心（2，2）到直线x=-1的距离为d=3＞r=1，可得直线和圆相离．再根据切线长|PQ|的最小值为$\sqrt{{d}^{2}-{r}^{2}}$，运算求得结果．

解答解：圆心（2，2）到直线x=-1的距离为d=3＞r=1，故直线和圆相离．
故切线长|PQ|的最小值为$\sqrt{9-1}$=2$\sqrt{2}$，
故选：B．

点评本题主要考查直线和圆的位置关系，点到直线的距离公式，求圆的切线长的方法，属于中档题．

练习册系列答案

相关题目

11．

如图1，以BD为直径的圆O经过A，C两点，延长DA，CB交于P点，如图2，将PAB沿线段AB折起，使P点在底面ABCD的射影恰为AD的中点Q，AB=BC=1，BD=2，线段PB，PC的中点为E，F．
（1）判断四点A，D，E，F是否共面，并说明理由；
（2）求四棱锥E-ABCQ的体积．

12．函数f（x）=sin（ln$\frac{x-1}{x+1}$）的图象大致为（　　）

	A．			B．
	C．			D．

9．定积分$\int_{-1}^1{[\sqrt{1-{x^2}}+cos（2x-\frac{π}{2}）]}dx$的值为$\frac{π}{2}$．

16．已知集合M={x|16-x²≥0}，集合N={y|y=|x|+1}，则M∩N=（　　）

6．

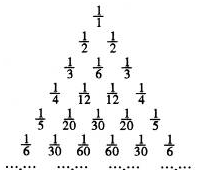德国数学家莱布尼兹发现了右面的单位分数三角形，单位分数是分子为1，分母为正整数的分数称为莱布尼兹三角形：根据前6行的规律，写出第7行的第3个数是$\frac{1}{105}$．

13．函数f（x）=ln（4-x）的定义域为（　　）

10．已知函数$f（x）=\frac{{{a^x}-1}}{{{a^x}+1}}（a＞1），g（x）={3^x}$．
（1）若g（a+2）=81，求实数a的值，并判断函数f（x）的奇偶性；
（2）用定义证明f（x）在R上的增函数；
（3）求函数f（x）的值域．

11．函数 f（x）=$\frac{1}{{\sqrt{3-x}}}$+ln（x+2）的定义域为（-2，3）．

试题分类