题目内容

17．已知抛物线C：y2=2px（p＞0）的焦点为F，A（4，y0）为抛物线C上一点，满足$|AF|=\frac{3}{2}p$，则p=（　　）
A．1B．2C．4D．8

分析 由抛物线的定义可知：丨AF丨=4+$\frac{p}{2}$，$|AF|=\frac{3}{2}p$，代入即可求得p的值．

解答 解：由题意可知：抛物线C：y2=2px（p＞0），焦点在x轴上，焦点坐标F（$\frac{p}{2}$，0），
由抛物线的定义可知：丨AF丨=4+$\frac{p}{2}$，$|AF|=\frac{3}{2}p$，
∴$\frac{3p}{2}$=4+$\frac{p}{2}$，则p=4，
故选C．

点评 本题考查抛物线的定义，属于基础题．

练习册系列答案
相关题目
7．已知函数f（x）=$\frac{{{e^x}-{e^{-x}}}}{{{e^x}+{e^{-x}}}}$．
（Ⅰ）证明：f（x）为奇函数；
（Ⅱ）判断f（x）单调性并证明；
（III）不等式f（x-t）+f（x2-t2）≥0对于x∈[1，2]恒成立，求实数t的取值范围．
8．若不等式组$\left\{\begin{array}{l}{x≥0}\\{x+y≥1}\\{3x+y≤3}\end{array}\right.$所表示的平面区域为D，若直线y-2=a（x+2）与D有公共点，则a的取值范围是$-\frac{2}{3}≤$a≤$\frac{1}{2}$．
5．已知直线a、b和平面α、β，下列命题中假命题的是①②③④（只填序号）．
①若a∥b，则a平行于经过b的任何平面；
②若a∥α，b∥α，则a∥b；
③若a∥α，b∥β，且α⊥β，则a⊥b；
④若α∩β=a，且b∥α，则b∥a．
12．函数f（x）=sin（ln$\frac{x-1}{x+1}$）的图象大致为（　　）
A．B．
C．D．
2．定义新运算：$|{\begin{array}{l}{a_1}&{a_2}\\{{a_3}}&{a_4}\end{array}}|={a_1}{a_4}-{a_2}{a_3}$，若函数$f（x）=|{\begin{array}{l}{\sqrt{3}cosx}&{-1}\\{{{sin}^2}x}&{sinx}\end{array}}|$，则下列结论不正确的是（　　）
A．函数y=f（x）的最小正周期为π
B．函数y=f（x）的一个对称中心为$（\frac{7π}{12}，\frac{1}{2}）$
C．函数y=f（x）在区间$[0，\frac{π}{2}]$上单调递增
D．将函数y=f（x）的图象向右平移$\frac{π}{6}$个单位后，所得图象对应的函数为偶函数
9．定积分$\int_{-1}^1{[\sqrt{1-{x^2}}+cos（2x-\frac{π}{2}）]}dx$的值为$\frac{π}{2}$．
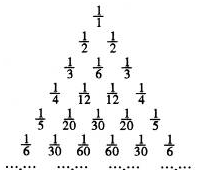6．德国数学家莱布尼兹发现了右面的单位分数三角形，单位分数是分子为1，分母为正整数的分数称为莱布尼兹三角形：根据前6行的规律，写出第7行的第3个数是$\frac{1}{105}$．
7．（1-x）（2x+1）4的展开式中，x3的系数为8．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网