题目内容
2．若圆锥曲线C：x2+my2=1的离心率为2，则m=（ ）| A． | $-\frac{{\sqrt{3}}}{3}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $-\frac{1}{3}$ | D． | $\frac{1}{3}$ |
分析 圆锥曲线C：x2+my2=1方程可化为${x^2}-\frac{y^2}{{-\frac{1}{m}}}=1（m＜0）$，利用离心率为2，求出m的值．
解答 解：因为圆锥曲线C：x2+my2=1方程可化为${x^2}-\frac{y^2}{{-\frac{1}{m}}}=1（m＜0）$，
所以离心率为$\sqrt{1+（-\frac{1}{m}）}=2⇒m=-\frac{1}{3}$，
故选：C．
点评 本题考查双曲线的离心率，考查方程思想，比较基础．
练习册系列答案
相关题目
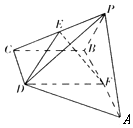如图，在四棱锥P-ABCD中底面ABCD是直角梯形，AB∥CD，∠ABC=90°，AB=2CD，BC=$\sqrt{3}$CD，△APB是等边三角形，且侧面APB⊥底面ABCD，E，F分别是PC，AB的中点．
如图1，以BD为直径的圆O经过A，C两点，延长DA，CB交于P点，如图2，将PAB沿线段AB折起，使P点在底面ABCD的射影恰为AD的中点Q，AB=BC=1，BD=2，线段PB，PC的中点为E，F．
