题目内容
2．若实数x，y满足约束条件$\left\{\begin{array}{l}{x≤1}\\{y≤2}\\{2x+y≥2}\end{array}$，则z=x2+y2的最小值是（ ）| A． | $\frac{2\sqrt{5}}{5}$ | B． | $\frac{4}{5}$ | C． | 1 | D． | 4 |
分析 由约束条件作出可行域，由z=x2+y2的几何意义，即原点O（0，0）到直线3x+4y-5=0的距离求得答案．
解答 
解：由约束条件$\left\{\begin{array}{l}{x≤1}\\{y≤2}\\{2x+y≥2}\end{array}$，作出可行域如图，
由图可知，z=x2+y2的最小值为原点O（0，0）
到直线2x+y-2=0的距离的平方，
等于$（\frac{2}{\sqrt{1+4}}）^{2}$=$\frac{4}{5}$．
故选：B．
点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
13．函数f（x）=ln（4-x）的定义域为（ ）
| A． | （-∞，4] | B． | （-∞，4） | C． | （0，4] | D． | （0，4） |
17．
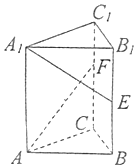在三棱柱ABC-A1B1C1中，底面为正三角形，侧棱垂直底面，AB=4，AA1=6．若E，F分别是棱BB1，CC1上的点，且$BE={B_1}E，{C_1}F=\frac{1}{3}C{C_1}$，则异面直线A1E与AF所成角的余弦值为（ ）
在三棱柱ABC-A1B1C1中，底面为正三角形，侧棱垂直底面，AB=4，AA1=6．若E，F分别是棱BB1，CC1上的点，且$BE={B_1}E，{C_1}F=\frac{1}{3}C{C_1}$，则异面直线A1E与AF所成角的余弦值为（ ）| A． | $-\frac{{\sqrt{2}}}{6}$ | B． | $\frac{{\sqrt{2}}}{6}$ | C． | $-\frac{{\sqrt{2}}}{10}$ | D． | $\frac{{\sqrt{2}}}{10}$ |