题目内容

方程|x|+
3
2
-x2
=
2
的根的个数为
 
 个．
考点：方根与根式及根式的化简运算
专题：函数的性质及应用
分析：要使
3
2
-x2
有意义，可得-
3
2
≤x≤
3
2
．当0≤x≤
3
2
时，原方程化为x+
3
2
-x2
=
2
；当-
3
2
≤x＜0时，原方程化为-x+
3
2
-x2
=
2
，分别解出即可．
解答： 解：要使
3
2
-x2
有意义，
则-
3
2
≤x≤
3
2
．
当0≤x≤
3
2
时，原方程化为x+
3
2
-x2
=
2
，
∴
3
2
-x2
=
2
-x，两边平方化为4x2-4
2
x+1=0，
解得x=
2
±1
2
，经过验证都满足题意．
当-
3
2
≤x＜0时，原方程化为-x+
3
2
-x2
=
2
，
∴
3
2
-x2
=
2
+x，两边平方化为4x2+4
2
+1=0，
解得x=
-
2
±1
2
，经过验证都满足题意．
综上可得：原方程由4个解．
点评：本题考查了根式方程、含绝对值的方程的解法，考查了分类讨论的思想方法，考查了推理能力月计算能力，属于中档题．
练习册系列答案
相关题目
设a=
3
-
2
，b=
6
-
5
，c=
7
-
6
，则a、b、c的大小顺序是
 
．
将函数y=sinx+cosx（x∈R）的图象向左平移m（m＞0）个单位长度后，得到图象关于y轴对称，则m的最小值为（　　）
A、
π
4
B、
π
3
C、
π
2
D、π
已知f（x）=
x+1，x∈[-1，0)
x2+1，x∈[0，1]
，则下列函数的图象错误的是（　　）
A、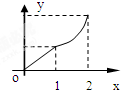
f（x-1）的图象
B、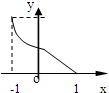
f（-x）的图象
C、
f（|x|）的图象
D、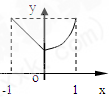
|f（x）|的图象
已知x+1是5和7的等差中项，则x的值为（　　）
A、5B、6C、8D、9
不等式3x+1＜92x-1的解集为
 
．
已知函数f（x）=2sinx（sinx+cosx）．
（1）求函数f（x）的最大值及相应的x值；
（2）试叙述：函数y=f（x）的图象可由函数y=sinx的图象经过怎样的变换而得到．
已知全集U=R，A={x|x＞1}，B={x|x2-2x＞0}，则∁U（A∪B）=（　　）
A、{x|x≤2}
B、{x|x≥1}
C、{x|0≤x≤1}
D、{x|0≤x≤2}
函数y=ln（x-2）的定义域是（　　）
A、（-∞，+∞）
B、（-∞，2）
C、（0，2）
D、（2，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网