题目内容
9.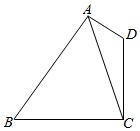 如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cosB=$\frac{\sqrt{3}}{3}$.
如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cosB=$\frac{\sqrt{3}}{3}$.(I)求△ACD的面积;
(Ⅱ)若BC=2$\sqrt{3}$,求AB的长.
分析 (1)利用已知条件求出D角的正弦函数值,然后求△ACD的面积;
(2)利用余弦定理求出AC,通过BC=2$\sqrt{3}$,利用正弦定理求解AB的长.
解答 解:(Ⅰ)cosD=cos2B=2cos2B-1=-$\frac{1}{3}$,…(2分)
因为∠D∈(0,π),所以sinD=$\frac{2\sqrt{2}}{3}$,…(4分)
所以△ACD的面积S=$\frac{1}{2}AD•CD•sinD$=$\frac{1}{2}×1×3×\frac{2\sqrt{2}}{3}$=$\sqrt{2}$.…(7分)
(Ⅱ)在△ACD中,AC2=AD2+DC2-2AD•DC•cosD=12,
所以AC=2$\sqrt{3}$.…(9分)
在△ABC中,BC=2$\sqrt{3}$,$\frac{AC}{sinB}=\frac{AB}{sin∠ACB}$,…(12分)
把已知条件代入并化简得:$\frac{2\sqrt{3}}{sinB}=\frac{AB}{sin(π-2B)}=\frac{AB}{\frac{2\sqrt{3}}{3}sinB}$,
所以AB=4.…(15分)
点评 本题考查余弦定理以及正弦定理的应用,基本知识的考查,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.设数列{an}满足:an+1=$\frac{1+{a}_{n}}{1-{a}_{n}}$,a2015=3,那么a1等于( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{3}$ | D. | 3 |
 函数y=sin(ωx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,若$cos∠APB=-\frac{{\sqrt{5}}}{5}$,则ω的值为$\frac{π}{2}$.
函数y=sin(ωx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,若$cos∠APB=-\frac{{\sqrt{5}}}{5}$,则ω的值为$\frac{π}{2}$.