题目内容
19．已知函数f（x）=2x3-6x2+m（m为常数）在[-2，2]上的最小值为-38，则f（x）在[-2，2]上的最大值是（ ）| A． | 1 | B． | -1 | C． | 2 | D． | -2 |
分析 先求导数，根据单调性研究函数的极值点，在开区间（-2，2）上只有一极大值则就是最大值，从而求出m，通过比较两个端点-2和2的函数值的大小从而确定出最小值，得到结论．
解答 解：∵f′（x）=6x2-12x=6x（x-2），
∵f（x）在（-2，0）上为增函数，在（0，2）上为减函数，
∴当x=0时，f（x）=m最大，
又f（-2）=m-40，f（2）=m-8，可得f（x）的最小值为f（-2）=-38，
∴m=2，
∴f（x）的最大值为2．
故选：C．
点评 本题考查了利用导数求闭区间上函数的最值，求函数在闭区间[a，b]上的最大值与最小值是通过比较函数在（a，b）内所有极值与端点函数f（a），f（b） 比较而得到的，属于基础题．
练习册系列答案
相关题目
10．已知双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的离心率为$\sqrt{2}$，且双曲线与抛物线x2=-4$\sqrt{3}$y的准线交于A，B，S△OAB=$\sqrt{3}$，则双曲线的实轴长（ ）
| A． | 2$\sqrt{2}$ | B． | 4$\sqrt{2}$ | C． | 2 | D． | 4 |
7．如图，在正方体ABCD-A′B′C′D′中，E为A′C′的中点，则异面直线CE与BD所成的角为（ ）
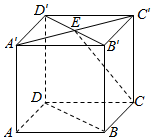
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
4．设等差数列{an}的前项和为Sn，若a1=-40，a6+a10=-10，则当Sn取得最小值时n的值为（ ）
| A． | 8或9 | B． | 9或10 | C． | 8 | D． | 9 |
11．函数$y={log_{\frac{1}{4}}}（{-{x^2}+2x+3}）$的单调增区间是（ ）
| A． | （-1，1] | B． | （-∞，1） | C． | [1，3） | D． | （1，+∞） |
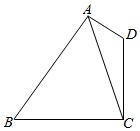如图所示，在四边形ABCD中，∠D=2∠B，且AD=1，CD=3，cosB=$\frac{\sqrt{3}}{3}$．