题目内容
17.已知在$f(x)={(\frac{1}{x}+{x^2})^n}$的展开式中,第4项为常数项(1)求f(x)的展开式中含x-3的项的系数;
(2)求f(x)的展开式中系数最大的项.
分析 (1)利用通项公式根据第4项为常数项,求得n的值,可得f(x)的展开式中含x-3的项的系数.
(2)根据通项公式可得f(x)的展开式中系数最大的项,即r=4,或r=5,从而得出结论.
解答 解:(1)在$f(x)={(\frac{1}{x}+{x^2})^n}$的展开式中,第4项为T4=${C}_{n}^{3}$•x9-n,为常数项,
∴n=9,故$f(x)={(\frac{1}{x}+{x^2})^n}$=${(\frac{1}{x}{+x}^{2})}^{9}$,它的通项公式为Tr+1=${C}_{9}^{r}$•x3r-9,
令3r-9=-3,求得r=2,可得f(x)的展开式中含x-3的项的系数为${C}_{9}^{2}$=36.
(2)f(x)的展开式中系数最大的项,即r=4,或r=5,
故系数最大的项为第五项或第六项,即T5=${C}_{9}^{4}$•x3,T6=${C}_{9}^{5}$•x9.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于基础题.

练习册系列答案
相关题目
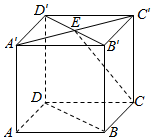
7.如图,在正方体ABCD-A′B′C′D′中,E为A′C′的中点,则异面直线CE与BD所成的角为( )

| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
12.$\frac{3+2i}{2-3i}$=( )
| A. | 1+i | B. | 1-i | C. | i | D. | -i |
7.雾霾影响人们的身体健康,越来越多的人开始关心如何少产生雾霾,春节前夕,某市健康协会为了了解公众对“适当甚至不燃放烟花爆竹”的态度,随机采访了50人,将凋查情况进行整理后制成下表:
(1)以赞同人数的频率为概率,若再随机采访3人,求至少有1人持赞同态度的概率;
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞同“适当甚至不燃放烟花爆竹”的人数为X,求随机变量X的分布列和数学期望.
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 12 | 7 | 3 | 3 |
(2)若从年龄在[15,25),[25,35)的被调查者中各随机选取两人进行追踪调查,记选中的4人中不赞同“适当甚至不燃放烟花爆竹”的人数为X,求随机变量X的分布列和数学期望.
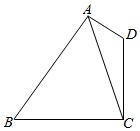 如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cosB=$\frac{\sqrt{3}}{3}$.
如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cosB=$\frac{\sqrt{3}}{3}$.