题目内容
已知圆心为C的圆经过点A(-1,1)和B(-2,-2),且圆心在直线l:x+y-1=0上.
(1)求圆心为C的圆的标准方程;
(2)若直线kx-y+5=0被圆C所截得的弦长为8,求k的值;
(3)设点P在圆C上,点Q在直线l:x-y+5=0上,求|PQ|的最小值.
(1)求圆心为C的圆的标准方程;
(2)若直线kx-y+5=0被圆C所截得的弦长为8,求k的值;
(3)设点P在圆C上,点Q在直线l:x-y+5=0上,求|PQ|的最小值.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)设圆的标准方程为(x-a)2+(y-b)2=r2,利用圆经过点A(-1,1)和B(-2,-2),且圆心在直线l:x+y-1=0上,建立方程组,求出a,b,r,即可得出圆心为C的圆的标准方程;
(2)根据直线kx-y+5=0被圆C所截得的弦长为8,求出圆心C到直线kx-y+5=0的距离,利用点到直线的距离公式,建立方程,即可求k的值;
(3)求出圆心C到直线x-y+5=0的距离,即可求|PQ|的最小值.
(2)根据直线kx-y+5=0被圆C所截得的弦长为8,求出圆心C到直线kx-y+5=0的距离,利用点到直线的距离公式,建立方程,即可求k的值;
(3)求出圆心C到直线x-y+5=0的距离,即可求|PQ|的最小值.
解答:
解:(1)设圆的标准方程为(x-a)2+(y-b)2=r2,则
∵圆经过点A(-1,1)和B(-2,-2),且圆心在直线l:x+y-1=0上,
∴
,
∴a=3,b=-2,r=5,
∴圆的标准方程为(x-3)2+(y+2)2=25;
(2)由条件可知:圆心C到直线kx-y+5=0的距离为d=
=3.…(8分)
根据点到直线的距离公式得
=3,…(10分)
解得:k=-
.…(11分)
(3)∵圆心C到直线x-y+5=0的距离为d=
=5
>5,…(12分)
∴直线与圆C相离,
∴|PQ|的最小值为d-r=5
-5…(14分)
∵圆经过点A(-1,1)和B(-2,-2),且圆心在直线l:x+y-1=0上,
∴
|
∴a=3,b=-2,r=5,
∴圆的标准方程为(x-3)2+(y+2)2=25;
(2)由条件可知:圆心C到直线kx-y+5=0的距离为d=
| 52-42 |
根据点到直线的距离公式得
| |3k+2+5| | ||
|
解得:k=-
| 20 |
| 21 |
(3)∵圆心C到直线x-y+5=0的距离为d=
| |3+2+5| | ||
|
| 2 |
∴直线与圆C相离,
∴|PQ|的最小值为d-r=5
| 2 |
点评:待定系数法是求圆的标准方程的重要方法,直线与圆的位置关系问题通常利用垂径定理解决.

练习册系列答案
相关题目
设A,B,C,D是平面直角坐标系中不同的四点,若
=λ
(λ∈R),
=μ
(μ∈R)且
+
=2,则称C,D是关于A,B的“好点对”.已知M,N是关于A,B的“好点对”,则下面说法正确的是( )
| AC |
| AB |
| AD |
| AB |
| 1 |
| λ |
| 1 |
| μ |
| A、M可能是线段AB的中点 |
| B、M,N可能同时在线段BA延长线上 |
| C、M,N可能同时在线段AB上 |
| D、M,N不可能同时在线段AB的延长线上 |
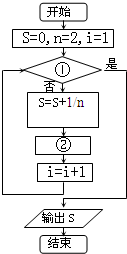
如图给出了计算
+
+
+…+
的值的程序框图,其中①②分别是( )
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 60 |

| A、i<30,n=n+2 |
| B、i=30,n=n+2 |
| C、i>30,n=n+2 |
| D、i>30,n=n+1 |