题目内容
20.已知F为抛物线C:y2=5x的焦点,点A(3,1),M是抛物线C上的动点,当|MA|+|MF|取最小值$\frac{17}{4}$时,点M的坐标为($\frac{1}{5}$,1).
分析 根据抛物线的定义,将|MA|+|MF|转化成|MA|+|PM|.由平面几何知识,可得当P、A、M三点共线时,|MA|+|PM|有最小值.由此即可得到|MA|+|MF|取最小值,进而得到相应的点M的坐标.
解答 解:由题意y2=5x得 F($\frac{5}{4}$,0),准线方程为 x=-$\frac{5}{4}$,点A(3,1),P(-$\frac{5}{4}$,1)
设点M到准线的距离为d=|PM|,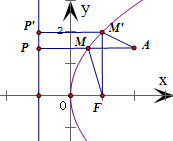
则由抛物线的定义得|MA|+|MF|=|MA|+|PM|,
故当P、A、M三点共线时,|MF|+|MA|取得最小值为|AP|=3-(-$\frac{5}{4}$)=$\frac{17}{4}$,
再将y=1代入抛物线y2=5x 得 x=$\frac{1}{5}$,故点M的坐标是:($\frac{1}{5}$,1).
故答案为:$\frac{17}{4}$,($\frac{1}{5}$,1)
点评 本题考查抛物线的定义和性质得应用,考查运算求解能力,考查数形结合思想,解答的关键利用是抛物线定义,体现了转化的数学思想.

练习册系列答案
相关题目
11.设变量x,y满足约束条件$\left\{\begin{array}{l}{2x+y≥4}\\{x-y≥1}\\{x-2y≤2}\end{array}\right.$,则x+2y的最小值为( )
| A. | -2 | B. | 1 | C. | 2 | D. | 3 |
8.已知等比数列{an}中,4a1,a3,2a2成等差数列,则公比q=( )
| A. | 2 | B. | -1或-2 | C. | -1或2 | D. | -1 |
15.设等差数列{an}与等比数列{bn}满足:0<a1=b1<a5=b5,则下述结论一定成立的是( )
| A. | a3<b3 | B. | a3>b3 | C. | a6<b6 | D. | a6>b6 |
5.在一次抽奖活动中,8张奖券中有一、二、三等奖各1张,其余5张无奖.甲、乙、丙、丁四名顾客每人从中抽取2张,则不同的获奖情况有( )
| A. | 24种 | B. | 36种 | C. | 60种 | D. | 96种 |
12.函数f(x)=sin(2x+φ)(|φ|<π)的图象向左平移$\frac{π}{3}$个单位后得到函数g(x)=-cos2x的图象,则函数 f(x)的图象( )
| A. | 关于直线x=$\frac{π}{12}$对称 | B. | 关于直线x=$\frac{5π}{12}$对称 | ||
| C. | 关于点($\frac{π}{12}$,0)对称 | D. | 关于点($\frac{5π}{12}$,0)对称 |