题目内容
8.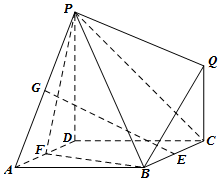 如图所示的多面体中,面ABCD是边长为2的正方形,平面PDCQ⊥平面ABCD,PD⊥DC,E,F,G分别为棱BC,AD,PA的中点.
如图所示的多面体中,面ABCD是边长为2的正方形,平面PDCQ⊥平面ABCD,PD⊥DC,E,F,G分别为棱BC,AD,PA的中点.(Ⅰ)求证:EG∥平面PDCQ;
(Ⅱ)已知二面角P-BF-C的余弦值为$\frac{\sqrt{6}}{6}$,求四棱锥P-ABCD的体积.
分析 (Ⅰ)取PD中点H,连接GH,HC,通过证明EG∥HC.然后证明EG∥平面PDCQ.
(Ⅱ)以D为原点,射线DA,DC,DP分别为x,y,z轴正方向,建立空间直角坐标系.设PD=a,求出相关点的坐标,求出平面ABCD的一个法向量,平面PFB的一个法向量,求出|cos$<\overrightarrow{m},\overrightarrow{n}>$|,推出PD,然后求解几何体的体积.
解答 (本小题共14分)
证明:(Ⅰ)取PD中点H,连接GH,HC,
因为ABCD是正方形,所以AD∥BC,AD=BC.
因为G,H分别是PA,PD中点,所以GH∥AD,$GH=\frac{1}{2}AD$.
又因为EC∥AD且$EC=\frac{1}{2}AD$,
所以GH∥EC,GH=EC,
所以四边形GHCE是平行四边形,….(3分)
所以EG∥HC.
又因为EG?平面PDCQ,HC?平面PDCQ
所以EG∥平面PDCQ. ….(5分)
解:(Ⅱ)因为平面PDCQ⊥平面ABCD,
平面PDCQ∩平面ABCD=CD,PD⊥DC,PD?平面PDCQ,
所以PD⊥平面ABCD. ….(6分)
如图,以D为原点,射线DA,DC,DP分别为x,y,z轴正方向,建立空间直角坐标系.
设PD=a,则 P(0,0,a),F(1,0,0),B(2,2,0).…(7分)
因为PD⊥底面ABCD,所以平面ABCD的一个法向量为$\overrightarrow{m}$=(0,0,1).….(8分)
设平面PFB的一个法向量为$\overrightarrow{n}$=(x,y,z),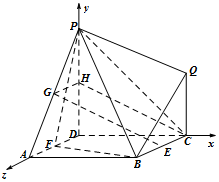
$\overrightarrow{PF}$=(1,0,-a),$\overrightarrow{FB}$=(1,2,0)
则$\left\{\begin{array}{l}{\overrightarrow{PF}•\overrightarrow{n}=0}\\{\overrightarrow{FB}•\overrightarrow{n}=0}\end{array}\right.$
即$\left\{{\begin{array}{l}{x-az=0}\\{x+2y=0}\end{array}}\right.$
令x=1,得$z=\frac{1}{a},y=-\frac{1}{2}$,所以$\overrightarrow{n}$=(1,-$\frac{1}{2}$,$\frac{1}{a}$) ….(10分)
由已知,二面角P-BF-C的余弦值为$\frac{{\sqrt{6}}}{6}$,
所以得|cos$<\overrightarrow{m},\overrightarrow{n}>$|=$|\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}|$=$\frac{|\frac{1}{a}|}{\sqrt{\frac{5}{4}+\frac{1}{{a}^{2}}}}$=$\frac{\sqrt{6}}{6}$,….(11分)
解得a=2,所以PD=2. ….(13分)
因为PD是四棱锥P-ABCD的高,
所以其体积为${V_{P-ABCD}}=\frac{1}{3}×2×4=\frac{8}{3}$. ….(14分)
点评 本题考查空间向量求解二面角的平面角,几何体的体积的求法,直线与平面平行的判断.考查空间想象能力以及计算能力.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案| A. | ∅ | B. | {2} | C. | {2,3} | D. | {x|2≤x<3} |
| A. | $\frac{1}{2}$或$\frac{11}{32}$ | B. | $\frac{1}{2}$或$\frac{31}{32}$ | C. | $\frac{11}{32}$或$\frac{31}{32}$ | D. | $\frac{11}{32}$或$\frac{5}{2}$ |
| A. | 三角形的边长与面积之间的关系 | |
| B. | 等边三角形的边长与面积之间的关系 | |
| C. | 四边形的边长与面积之间的关 | |
| D. | 菱形的边长与面积之间的关 |
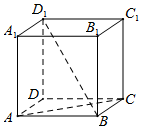 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.