题目内容
20.已知定义在[1,+∞)上的函数$f(x)=\left\{\begin{array}{l}4-8|{x-\frac{3}{2}}|,1≤x≤2\\ \frac{1}{2}f({\frac{x}{2}}),x>2\end{array}\right.$,当x∈[2n-1,2n](n∈N*)时,函数f(x)的图象与x轴围成的图象面积为Sn,则S1+S2+…+Sn=( )| A. | 2n | B. | 2n | C. | 2n+1-2 | D. | n2+n |
分析 作出函数f(x)的图象,求出三角形的高,结合三角形的面积公式进行求解即可.
解答 解:作出函数f(x)在[1,+∞)上的图象如图: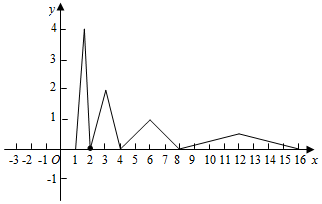
当n=1时,x∈[1,2],此时三角形的高为f($\frac{3}{2}$)=4,则S1=$\frac{1}{2}$×1×4=2,
当n=2时,x∈[2,4],此时三角形的高为f(3)=$\frac{1}{2}$f($\frac{3}{2}$)=$\frac{1}{2}×$4=2,则S2=$\frac{1}{2}$×2×2=2,
当n=3时,x∈[4,8],此时三角形的高为f(6)=$\frac{1}{2}$f(3)=$\frac{1}{2}×$2=1,则S3=$\frac{1}{2}$×4×1=2,
综上当x∈[2n-1,2n](n∈N*)时,函数f(x)的最高点为23-n,与x轴围成的面积为Sn=$\frac{1}{2}$×23-n×2n-1=2.
则S1+S2+…+Sn=2+2+…+2=2n,
故选:B
点评 本题主要考查分段函数的应用,根据分段函数作出函数的图象,求出对应三角形的高,结合三角形的面积公式是解决本题的关键.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
11.如复数z满足:z+1=(z-1)i,则复数z的共轭复数$\overline{z}$等于( )
| A. | -i | B. | i | C. | 1-i | D. | 1+i |