题目内容
8.方程z=$\sqrt{1-{x}^{2}-{y}^{2}}$的几何意义表示空间中以原点为球心,以1为半径的上半球面.分析 把已知等式两边平方,变形后可得x2+y2+z2=1(z≥0),由此可得方程z=$\sqrt{1-{x}^{2}-{y}^{2}}$的几何意义.
解答 解:由z=$\sqrt{1-{x}^{2}-{y}^{2}}$,得z2=1-x2-y2(z≥0),
即x2+y2+z2=1(z≥0),
∴方程z=$\sqrt{1-{x}^{2}-{y}^{2}}$的几何意义表示空间中以原点为球心,以1为半径的上半球面.
故答案为:空间中以原点为球心,以1为半径的上半球面.
点评 本题考查曲线方程,考查了数学转化思想方法,是中档题.

练习册系列答案
相关题目
18.函数y=logax(a>0且a≠1)的反函数的图象经过点(2,4),则a的值为( )
| A. | 2 | B. | 4 | C. | $\frac{1}{2}$ | D. | $\sqrt{2}$ |
16.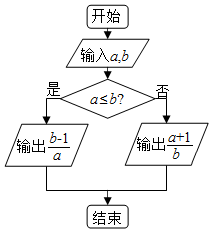 若对任意非零实数a,b,若a*b的运算规则如图的程序框图所示,则(3*2)*4的值是( )
若对任意非零实数a,b,若a*b的运算规则如图的程序框图所示,则(3*2)*4的值是( )
 若对任意非零实数a,b,若a*b的运算规则如图的程序框图所示,则(3*2)*4的值是( )
若对任意非零实数a,b,若a*b的运算规则如图的程序框图所示,则(3*2)*4的值是( )| A. | $\frac{13}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | 9 |
3.某程序的框图如图所示,若输入的z=i(其中i为虚数单位),则输出的S 值为( )

| A. | -1 | B. | 1 | C. | -i | D. | i |
13.执行如图所示的程序框图,则输出的结果是( )


| A. | 30 | B. | 120 | C. | 360 | D. | 720 |
20.已知定义在[1,+∞)上的函数$f(x)=\left\{\begin{array}{l}4-8|{x-\frac{3}{2}}|,1≤x≤2\\ \frac{1}{2}f({\frac{x}{2}}),x>2\end{array}\right.$,当x∈[2n-1,2n](n∈N*)时,函数f(x)的图象与x轴围成的图象面积为Sn,则S1+S2+…+Sn=( )
| A. | 2n | B. | 2n | C. | 2n+1-2 | D. | n2+n |
17.MOD(a.b)表示求a除以b的余数,若输入a=34,b=85,则输出的结果为( )>
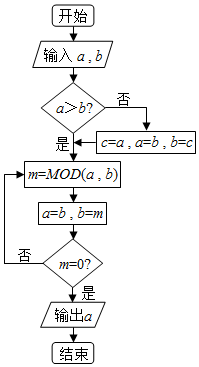

| A. | 0 | B. | 17 | C. | 21 | D. | 34 |