题目内容
12．设x，y满足条件：$\left\{\begin{array}{l}x-y+2≥0\\ 2x+y-5≥0\\ 2x-y-3≤0\end{array}\right.$，则z=3x+2y的最大值为（ ）| A． | 8 | B． | 9 | C． | 28 | D． | 29 |
分析 作出可行域，将目标函数变形得y=-$\frac{3}{2}$x+$\frac{z}{2}$，寻找直线截距最大时的最优解．
解答 解：作出约束条件表示的可行域如图：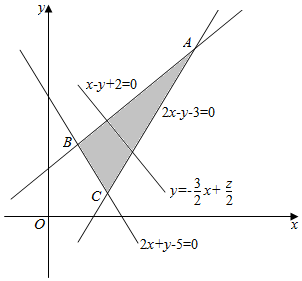
由目标函数z=3x+2y得y=-$\frac{3}{2}x$+$\frac{z}{2}$．
由图形可知当直线y=-$\frac{3}{2}x$+$\frac{z}{2}$过点A时，截距最大，即z最大．
解方程组$\left\{\begin{array}{l}{x-y+2=0}\\{2x-y-3=0}\end{array}\right.$得x=5，y=7，即A（5，7），
∴z的最大值为3×5+2×7=29．
故选D．
点评 本题考查了简单的线性规划，结合图形寻找最优解是关键，属于中档题．
练习册系列答案
导学全程练创优训练系列答案
相关题目
3．已知函数y=f（x）的图象是由y=sin2x向右平移$\frac{π}{12}$得到，则下列结论正确的是（ ）
| A． | f（0）＜f（2）＜f（4） | B． | f（2）＜f（0）＜f（4） | C． | f（0）＜f（4）＜f（2） | D． | f（4）＜f（2）＜f（0） |
17．函数$f（x）=\sqrt{x+3}+\frac{1}{x+1}$的定义域是（ ）
| A． | （-∞，-1）∪（-1，+∞） | B． | [-3，+∞） | C． | [-3，-1）∪（-1，+∞） | D． | （-1，+∞） |
如图，已知四棱锥P-ABCD，底面ABCD为正方形，PA⊥平面ABCD．
1．下列结论错误的是（ ）
| A． | 命题“若p，则q”与命题“若非q，则非p”互为逆否命题 | |
| B． | 命题p：?x∈R，e|x|≥1，命题q：?x∈R，x2+x+1＜0，则p∨q为真 | |
| C． | “若x为y=f（x）的极值点，则f′（x）=0”的逆命题为真命题 | |
| D． | 若“p且q”为真命题，则p、q均为真命题 |
2．已知A（-1，0）、B（2，1）、C（5，-8），△ABC的外接圆在点A处的切线为l，则点B到直线l的距离为（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | 1 | C． | $\sqrt{2}$ | D． | $\frac{5}{2}$ |