题目内容
4. 如图,已知四棱锥P-ABCD,底面ABCD为正方形,PA⊥平面ABCD.
如图,已知四棱锥P-ABCD,底面ABCD为正方形,PA⊥平面ABCD.给出下列命题:
①PB⊥AC;
②平面PAB与平面PCD的交线与AB平行;
③平面PBD⊥平面PAC;
④△PCD为锐角三角形.
其中正确命题的序号是②③.(写出所有正确命题的序号)
分析 AC∩BD=O,由题意证明AC⊥PO,由已知可得AC⊥PA,与在同一平面内过一点有且只有一条直线与已知直线垂直矛盾说明①错误;
由线面平行的判定和性质说明②正确;
由线面垂直的判定和性质说明③正确;
由勾股定理即可判断,说明④错误.
解答 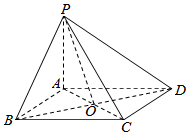 解:如图,
解:如图,
①、若PB⊥AC,∵AC⊥BD,则AC⊥平面PBD,∴AC⊥PO,
又PA⊥平面ABCD,则AC⊥PA,在平面PAC内过P有两条直线与AC垂直,与在同一平面内过一点有且只有一条直线与已知直线垂直矛盾.①错误;
②、∵CD∥AB,则CD∥平面PAB,∴平面PAB与平面PCD的交线与AB平行.②正确;
③、∵PA⊥平面ABCD,∴平面PAC⊥平面ABCD,
又BD⊥AC,∴BD⊥平面PAC,则平面PBD⊥平面PAC.③正确;
④、∵PD2=PA2+AD2,PC2=PA2+AC2,AC2=AD2+CD2,AD=CD,
∴PD2+CD2=PC2,
∴④△PCD为直角三角形,④错误,
故答案为:②③
点评 本题考查命题的真假判断与应用,考查了空间中直线和平面的位置关系,是中档题.

练习册系列答案
相关题目
12.设x,y满足条件:$\left\{\begin{array}{l}x-y+2≥0\\ 2x+y-5≥0\\ 2x-y-3≤0\end{array}\right.$,则z=3x+2y的最大值为( )
| A. | 8 | B. | 9 | C. | 28 | D. | 29 |
19.某位同学在2015年5月进行社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了5月1日至5月5日的白天平均气温x(°C)与该奶茶店的这种饮料销量y(杯),得到如下数据:
(1)若从这五组数据中随机抽出2组,求抽出的2组数据不是相邻2天数据的概率;
(2)请根据所给五组数据,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$.
(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
| 日 期 | 5月1日 | 5月2日 | 5月3日 | 5月4日 | 5月5日 |
| 平均气温x(°C) | 9 | 10 | 12 | 11 | 8 |
| 销量y(杯) | 23 | 25 | 30 | 26 | 21 |
(2)请根据所给五组数据,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$.
(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$)
13.过抛物线y2=4x的焦点的直线与抛物线交于A,B两个不同的点,当|AB|=6时,△OAB(O为坐标原点)的面积是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{6}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |