题目内容
6.已知函数f(x)=$\sqrt{3}$asinωx-acosωx(a>0,ω>0)的图象上的一个最高点和相邻的一个最低点坐标分别为$(\frac{π}{6},2),(\frac{2π}{3},-2)$.(1)求a、ω的值;
(2)在△ABC中,a、b、c分别是角A、B、C的对边$(a<b),且f(A-\frac{π}{6})=1,求\frac{b-2c}{{asin(\frac{π}{6}-C)}}$.
分析 (1)利用三角恒等变换化简函数f(x)的解析式,由最值求出a的值,由周期求出ω,可得f(x)的解析式.
(2)由f($\frac{π}{6}$-A)=1求得sin(2A-$\frac{π}{2}$)=$\frac{1}{2}$,再根据a<b求得A必定为锐角,求得A的值.再利用正弦定理的应用以及三角恒等变换,求得要求式子的值.
解答 解:(1)∵函数f(x)=$\sqrt{3}$asinωx-acosωx=2a($\frac{\sqrt{3}}{2}$sinωx-$\frac{1}{2}$cosωx)=2asin(ωx-$\frac{π}{6}$)的图象上的一个最高点和相邻的一个最低点坐标分别为$(\frac{π}{6},2),(\frac{2π}{3},-2)$,
∴2a=2,a=1;$\frac{T}{2}$=$\frac{π}{ω}$=$\frac{2π}{3}$-$\frac{π}{6}$=$\frac{π}{2}$,∴ω=2.
(2)由(1)可得f(x)=2sin(2x-$\frac{π}{6}$),∵f(A-$\frac{π}{6}$)=2sin[2(A-$\frac{π}{6}$)-$\frac{π}{6}$]=2sin(2A-$\frac{π}{2}$)=1,
∴sin(2A-$\frac{π}{2}$)=$\frac{1}{2}$,
由a<b可得A必定为锐角,∴2A-$\frac{π}{6}$=$\frac{π}{6}$,∴A=$\frac{π}{3}$.
∴$\frac{b-2c}{asin(\frac{π}{6}-C)}$=$\frac{sinB-2sinC}{sinA•sin(\frac{π}{6}-C)}$=$\frac{sin(\frac{2π}{3}-C)-2sinC}{\frac{\sqrt{3}}{2}sin(\frac{π}{6}-C)}$=$\frac{\sqrt{3}sin(\frac{π}{6}-C)}{\frac{\sqrt{3}}{2}sin(\frac{π}{6}-C)}$=2.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由最值求出a的值,由周期求出ω,正弦函数的图象,正弦定理的应用以及三角恒等变换,属于中档题.

 阅读快车系列答案
阅读快车系列答案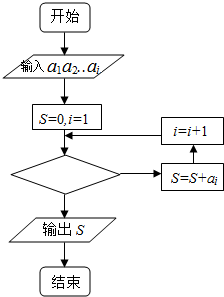 某篮球队6名主力队员在最近三场比赛中投进的三分球个数如表所示:
某篮球队6名主力队员在最近三场比赛中投进的三分球个数如表所示:| 队员i | 1 | 2 | 3 | 4 | 5 | 6 |
| 三分球个数ai | 9 | 13 | 11 | 7 | 5 | 6 |
| A. | 0∈∅ | B. | 1∈{偶数} | C. | 0∈{x|0<x<4} | D. | 2∈{x|x2-4=0} |
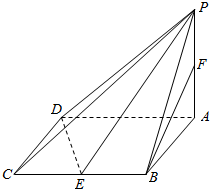 在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PA⊥面ABCD,PA=$\sqrt{3}$,E,F分别为BC,PA的中点.
在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,PA⊥面ABCD,PA=$\sqrt{3}$,E,F分别为BC,PA的中点.