题目内容
7.已知数列{an}满足2anan+1=an-an+1,且a1=$\frac{1}{2}$,n∈N+.(1)求数列{an}的通项公式;
(2)设数列{bn}的前n项和为Sn,若数列{bn}满足bn=$\left\{\begin{array}{l}{\frac{1}{\sqrt{n-1}+\sqrt{n+1}}(n=2k-1)}\\{{a}_{\frac{n}{2}}{a}_{\frac{n}{2}+1}(n=2k)}\end{array}\right.$(k∈N+),求S64;
(3)设Tn=$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{n}}$,是否存在实数c,使{$\frac{{T}_{n}}{n+c}$}为等差数列,请说明理由.
分析 (1)通过对2anan+1=an-an+1变形可知2=$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$,进而可知数列{$\frac{1}{{a}_{n}}$}是首项为2、公差为2的等差数列,计算即得结论;
(2)通过(1)裂项可知anan-1=$\frac{1}{4}$($\frac{1}{n}$-$\frac{1}{n+1}$),结合$\frac{1}{\sqrt{n-1}+\sqrt{n+1}}$=$\frac{\sqrt{n+1}-\sqrt{n-1}}{2}$,进而并项相加即得结论;
(3)通过(1)可知Tn=n(n+1),进而只需$\frac{{T}_{n}}{n+c}$变为关于n的一次函数,分c=0或c=1两种情况讨论即可.
解答 解:(1)∵2anan+1=an-an+1,
∴2=$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$,
又∵a1=$\frac{1}{2}$,即$\frac{1}{{a}_{1}}$=2,
∴数列{$\frac{1}{{a}_{n}}$}是首项为2、公差为2的等差数列,
故其通项公式an=$\frac{1}{2+2(n-1)}$=$\frac{1}{2n}$;
(2)由(1)可知anan-1=$\frac{1}{2n(2n+2)}$=$\frac{1}{4}$($\frac{1}{n}$-$\frac{1}{n+1}$),
又∵$\frac{1}{\sqrt{n-1}+\sqrt{n+1}}$=$\frac{\sqrt{n+1}-\sqrt{n-1}}{2}$,
∴S64=($\frac{\sqrt{2}-0}{2}$+$\frac{\sqrt{4}-\sqrt{2}}{2}$+…+$\frac{\sqrt{64}-\sqrt{62}}{2}$)+$\frac{1}{4}$(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{32}$-$\frac{1}{33}$)
=4+$\frac{1}{4}$(1-$\frac{1}{33}$)
=$\frac{140}{33}$;
(3)由(1)可知Tn=$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{n}}$
=2(1+2+…+n)
=n(n+1),
要使{$\frac{{T}_{n}}{n+c}$}为等差数列,则只需$\frac{{T}_{n}}{n+c}$变为关于n的一次函数,
则n+c可能为n或n+1,此时c=0或c=1,
当c=0时,{$\frac{{T}_{n}}{n+c}$}是首项为2、公差为1的等差数列;
当c=1时,{$\frac{{T}_{n}}{n+c}$}是首项为1、公差为1的等差数列;
综上所述,存在c=0或c=1满足题意.
点评 本题考查数列的通项及前n项和,考查裂项相消法,考查分类讨论的思想,注意解题方法的积累,属于中档题.

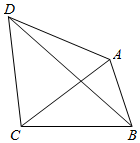 如图所示在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD的面积的最大值为$\sqrt{3}$+1.
如图所示在平面四边形ABCD中,AB=1,BC=2,△ACD为正三角形,则△BCD的面积的最大值为$\sqrt{3}$+1.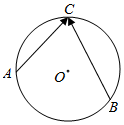 如图,⊙O是以O为圆心、1为半径的圆,设点A,B,C为⊙O上的任意三点,则$\overrightarrow{AC}$•$\overrightarrow{BC}$的取值范围为[-4,4].
如图,⊙O是以O为圆心、1为半径的圆,设点A,B,C为⊙O上的任意三点,则$\overrightarrow{AC}$•$\overrightarrow{BC}$的取值范围为[-4,4].