题目内容
17.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+2x,x≤0}\\{f(x-1)+1,x>0}\end{array}\right.$,当x∈[0,3]时,方程f(x)=x的所有根之和为6.分析 先根据函数式得出,当x∈(n,n+1]时,f(x)=(x-n)2+n,再画出两函数的图象,根据图象得出方程的根,再求和即可.
解答 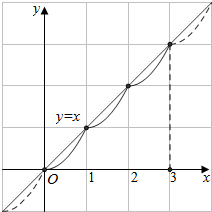 解:当x≤0时,f(x)=x2+2x=(x+1)2-1,所以,
解:当x≤0时,f(x)=x2+2x=(x+1)2-1,所以,
当x∈(0,1]时,f(x)=f(x-1)+1=x2,
当x∈(1,2]时,f(x)=f(x-1)+1=(x-1)2+1,
当x∈(2,3]时,f(x)=f(x-1)+1=(x-2)2+2,
…
当x∈(n,n+1]时,f(x)=f(x-1)+1=(x-n)2+n,
函数图象如右图所示,再画出y=x的图象,
由图可知,当x∈[0,3]时,两图象共有四个交点,
分别为:(0,0),(1,1),(2,2),(3,3),
即四个根为:x1=0,x2=1,x3=2,x4=3,
因此,所有根的和为:x1+x2+x3+x4=6,
故答案为:6.
点评 本题主要考查了分段函数解析式的确定与根的个数判断,涉及二次函数的图象与性质,体现了数形结合的解题思想,属于中档题.

练习册系列答案
相关题目
7.已知A(x1,y1),B(x2,y2)(x1>x2)是函数f(x)=ln|x|图象上的两个不同点,且在A,B两点处的切线互相垂直,则x1-x2的取值范围为( )
| A. | (0,+∞) | B. | (0,2) | C. | [1,+∞) | D. | [2,+∞) |
12.设x,y∈R,则“x,y≥1”是“x2+y2≥2”的( )
| A. | 既不充分也不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 充分不必要条件 |
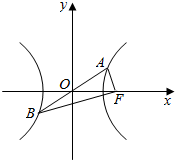 如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上有一点A,它关于原点的对称点为B,点F为是双曲线的右焦点,且满足AF⊥BF,设∠ABF=α,α∈[$\frac{π}{12}$,$\frac{π}{6}$],则该双曲线离心率e的取值范围为[$\sqrt{2}$,$\sqrt{3}$+1].
如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上有一点A,它关于原点的对称点为B,点F为是双曲线的右焦点,且满足AF⊥BF,设∠ABF=α,α∈[$\frac{π}{12}$,$\frac{π}{6}$],则该双曲线离心率e的取值范围为[$\sqrt{2}$,$\sqrt{3}$+1].