题目内容
已知实数x，y满足不等式组
，且z=x-y的最小值为-3，则实数m的值为（ ）
|
| A、-1 | ||
B、-
| ||
| C、6 | ||
| D、7 |
考点：简单线性规划
专题：不等式的解法及应用
分析：先作出不等式组对应的平面区域，利用z=x-y的最小值为-3，建立条件关系即可求实数m的值．
解答：
解：
由z=x-y得y=x-z，
由图象可知要使z=x-y的最小值为-3，
即y=x+3，此时直线y=x+3对应区域的截距最大，
由
，解得
，
即A（0，3），
同时A也在直线x+2y=m上，
即m=6，
故选：C．
由z=x-y得y=x-z，由图象可知要使z=x-y的最小值为-3，
即y=x+3，此时直线y=x+3对应区域的截距最大，
由
|
|
即A（0，3），
同时A也在直线x+2y=m上，
即m=6，
故选：C．
点评：本题主要考查线性规划的应用，利用目标函数取得最小值得到平面区域的对应关系是解决本题的关键．
练习册系列答案
相关题目
设实数x、y满足
，则z=max{2x+3y-1，x+2y+2}的取值范围是（ ）
|
| A、[2，5] |
| B、[2，9] |
| C、[5，9] |
| D、[-1，9] |
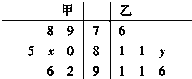甲、乙两中学各选出7名高一学生参加数学竞赛，他们取得的成绩的茎叶图如图，其中甲校学生成绩的众数是80，乙校学生成绩的中位数是86，则x+y的值为（ ）
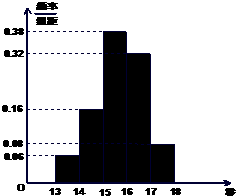某班50名学生在一次百米测试中，成绩全部介于13秒与18秒之间，将测试结果按如下方式分成五组：第一组[13，14），第二组[14，15）