题目内容
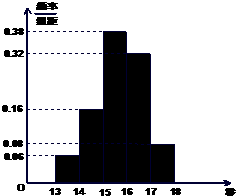 某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15)
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],下图是按上述分组方法得到的频率分布直方图.
(1)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(2)估计该组成绩的中位数(保留到小数点后两位)
(3)假设第一、五组中任意两个学生成绩都不相同,若从第一、五组所有成绩中随机取出两个,求这两个成绩分别来自不同组的概率.
考点:频率分布直方图,古典概型及其概率计算公式
专题:图表型,概率与统计
分析:(1)根据频率=小矩形的面积,求出成绩大于或等于14秒且小于16秒的频率,再利用频数=频率×样本容量求出答案;
(2)根据中位数的左右两边的小矩形的面积均为0.5,设出中位数,计算从左数面积=0.5的矩形的底边横坐标的值;
(3)求出第一组和第五组的人数,利用组合数公式求出从第一、五组所有成绩中随机取出两个的抽法种数及其中两个成绩分别来自不同组的抽法种数,根据古典概型概率公式计算.
(2)根据中位数的左右两边的小矩形的面积均为0.5,设出中位数,计算从左数面积=0.5的矩形的底边横坐标的值;
(3)求出第一组和第五组的人数,利用组合数公式求出从第一、五组所有成绩中随机取出两个的抽法种数及其中两个成绩分别来自不同组的抽法种数,根据古典概型概率公式计算.
解答:
解:(1)由频率分布直方图知成绩大于或等于14秒且小于16秒的频率为0.16+0.38=0.54,
∴百米测试中成绩良好的人数为50×0.54=27;
(2)第一组的频率为0.06,
第二组的频率为0.16,
第三组的频率为0.38,
∴中位数位于第三组,设中位数为15+x,则x×0.38=0.5-0.06-0.16=0.28,
∴x=0.74,∴中位数为15.74;
(3)第一组有0.06×50=3人;
第五组有0.08×50=4人,
从第一、五组所有成绩中随机取出两个共有
=21种方法,
其中两个成绩分别来自不同组的抽法有
=12种,
∴两个成绩分别来自不同组的概率为
=
.
∴百米测试中成绩良好的人数为50×0.54=27;
(2)第一组的频率为0.06,
第二组的频率为0.16,
第三组的频率为0.38,
∴中位数位于第三组,设中位数为15+x,则x×0.38=0.5-0.06-0.16=0.28,
∴x=0.74,∴中位数为15.74;
(3)第一组有0.06×50=3人;
第五组有0.08×50=4人,
从第一、五组所有成绩中随机取出两个共有
| C | 2 7 |
其中两个成绩分别来自不同组的抽法有
| C | 1 3 |
| ×C | 1 4 |
∴两个成绩分别来自不同组的概率为
| 12 |
| 21 |
| 4 |
| 7 |
点评:本题考查了频率分布直方图及利用频率分布直方图求中位数,考查了古典概型的概率计算,在频率分布直方图中频率=
=小矩形的面积=小矩形的高
| 频数 |
| 样本容量 |

练习册系列答案
相关题目
已知实数x,y满足不等式组
,且z=x-y的最小值为-3,则实数m的值为( )
|
| A、-1 | ||
B、-
| ||
| C、6 | ||
| D、7 |
下列说法错误的是( )
| A、如果直线上的两点在一个平面内,那么此直线在平面内 |
| B、过空间中三点,有且只有一个平面 |
| C、若两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线 |
| D、平行于同一条直线的两条直线互相平行 |
若曲线f(x)=xsinx+1在x=
处的切线与直线ax+2y+1=0互相垂直,则(ax2-
)5展开式中x的系数为( )
| π |
| 2 |
| 1 |
| x |
| A、40 | B、-10 |
| C、10 | D、-40 |
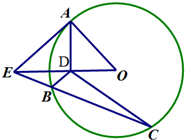 如图,AE是圆O的切线,A是切点,AD⊥OE于D,割线EC交圆O于B、C两点.
如图,AE是圆O的切线,A是切点,AD⊥OE于D,割线EC交圆O于B、C两点.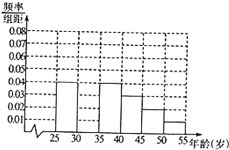 某同学在寒假期间进行社会实践活动,对[25,55]岁的人群随机抽取行人进行了一次生活习惯是否符合环保观念的调查,若生活习惯符合环保观念的称为“环保族”,否则称为“非环保族”,得到如下统计表和各年龄段人数的频率分布直方图:
某同学在寒假期间进行社会实践活动,对[25,55]岁的人群随机抽取行人进行了一次生活习惯是否符合环保观念的调查,若生活习惯符合环保观念的称为“环保族”,否则称为“非环保族”,得到如下统计表和各年龄段人数的频率分布直方图: