题目内容
以双曲线
-y2=1的右焦点为焦点,顶点在原点的抛物线标准方程是( )
| x2 |
| 3 |
| A、y2=4x |
| B、y2=-4x |
| C、y2=8x |
| D、y2=-8x |
考点:抛物线的标准方程,双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:先根据双曲线的方程求得其右焦点的坐标,进而设出抛物线的标准方程求得p,则抛物线的方程可得.
解答:
解:∵双曲线
-y2=1,
∴c=
=2,
∴双曲线的右焦点为:(2,0),
设抛物线的标准方程为y2=2px,
则
=2,p=4
∴抛物线标准方程为y2=8x,
故选C.
| x2 |
| 3 |
∴c=
| 3+1 |
∴双曲线的右焦点为:(2,0),
设抛物线的标准方程为y2=2px,
则
| p |
| 2 |
∴抛物线标准方程为y2=8x,
故选C.
点评:本题主要考查了抛物线的标准方程问题.较为基础,属基础题.

练习册系列答案
相关题目
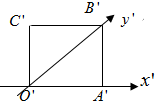 如图所示,正方形O′A′B′C′的边长2cm,它是水平放置的一个平面图形的直观图,则原图形的周长是( )
如图所示,正方形O′A′B′C′的边长2cm,它是水平放置的一个平面图形的直观图,则原图形的周长是( )| A、16cm | ||
| B、8cm | ||
C、(2+3
| ||
D、(2+2
|
设随机变量ξ服从正态分布N(0,σ2),若P(ξ<-1)=0.2,则P(-1<ξ<1)=( )
| A、0.2 | B、0.3 |
| C、0.4 | D、0.6 |
复数z=
,|
|是( )
| 5 |
| 3+4i |
. |
| z |
| A、25 | B、5 | C、1 | D、7 |
不等式(
-x)(x-
)>0的解集为( )
| 1 |
| 2 |
| 1 |
| 3 |
A、{x|
| ||||
B、{x|x>
| ||||
C、{x|x<
| ||||
D、{x|x<
|
函数f(x)=lnx+
的零点所在的区间是( )
| 1 |
| 2 |
| A、(e-4,e-2) |
| B、(e-2,1) |
| C、(1,e2) |
| D、(e2,e4) |
等差数列{an}中,a1+a5=6,a6=5,那么a9的值是( )
| A、-7 | ||
| B、7 | ||
C、-
| ||
D、
|