题目内容
求函数f（x）=
的单调区间．
| 3 | x2 |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：通过求导得出f′（x）=
，解不等式，从而得出函数的单调区间
| 2 | |||
3
|
解答：
解：∵f′（x）=
，
x＞0时，f′（x）＞0，
x＜0时，f′（x）＜0，
∴f（x）在（-∞，0）递减，在（0，+∞）递增．
| 2 | |||
3
|
x＞0时，f′（x）＞0，
x＜0时，f′（x）＜0，
∴f（x）在（-∞，0）递减，在（0，+∞）递增．
点评：本题考查了函数的单调性，考查导数的应用，是一道基础题．
练习册系列答案
相关题目
sin
的值等于（ ）
| 11π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
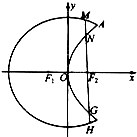我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”．如图，“盾圆C”是由椭圆