题目内容
函数f（x）=2sin（
-2x+φ），（0≤φ≤π）．
（1）当φ=0时，写出f（x）的递增区间；
（2）若f（x）是奇函数，求φ的值；
（3）f（x）的图象有一条对称轴x=
，求φ的值；
（4）f（x）的图象由y=-2sin2x的图象向右平移
个单位得到，求φ的值．
| π |
| 3 |
（1）当φ=0时，写出f（x）的递增区间；
（2）若f（x）是奇函数，求φ的值；
（3）f（x）的图象有一条对称轴x=
| π |
| 3 |
（4）f（x）的图象由y=-2sin2x的图象向右平移
| π |
| 4 |
考点：函数y=Asin（ωx+φ）的图象变换,正弦函数的图象
专题：三角函数的图像与性质
分析：（1）直接由复合函数的单调性求f（x）的递增区间；
（2）根据函数为奇函数，由f（0）=0求得φ的值；
（3）由f(
)=±2求得φ的值；
（4）求出y=-2sin2x的图象向右平移
个单位得到图象对应的函数解析式，由两函数解析式相同列式求得φ的值．
（2）根据函数为奇函数，由f（0）=0求得φ的值；
（3）由f(
| π |
| 3 |
（4）求出y=-2sin2x的图象向右平移
| π |
| 4 |
解答：
解：（1）φ=0时，f（x）=2sin（
-2x）=-2sin（2x-
），
由
+2kπ≤2x-
≤
+2kπ，得
+kπ≤x≤
+kπ，k∈Z．
∴f（x）的递增区间为[
+kπ，
+kπ]，k∈Z；
（2）∵f（x）=2sin（
-2x+φ）为奇函数，
∴f（0）=0，即sin（
+φ）=0．
∵0≤φ≤π，
∴φ=
；
（3）∵f（x）的图象有一条对称轴x=
，则f(
)=2sin(
-2×
+φ)=±2．
即sin（φ-
）=±1．
∵0≤φ≤π，
∴φ=
；
（4）由y=-2sin2x的图象向右平移
个单位，得到y=-2sin2（x-
）．
f（x）=2sin（
-2x+φ）=-2sin（2x-φ-
）．
∴-φ-
=-
．
φ=
．
| π |
| 3 |
| π |
| 3 |
由
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| 5π |
| 12 |
| 11π |
| 12 |
∴f（x）的递增区间为[
| 5π |
| 12 |
| 11π |
| 12 |
（2）∵f（x）=2sin（
| π |
| 3 |
∴f（0）=0，即sin（
| π |
| 3 |
∵0≤φ≤π，
∴φ=
| 2π |
| 3 |
（3）∵f（x）的图象有一条对称轴x=
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
即sin（φ-
| π |
| 3 |
∵0≤φ≤π，
∴φ=
| 5π |
| 6 |
（4）由y=-2sin2x的图象向右平移
| π |
| 4 |
| π |
| 4 |
f（x）=2sin（
| π |
| 3 |
| π |
| 3 |
∴-φ-
| π |
| 3 |
| π |
| 2 |
φ=
| π |
| 6 |
点评：本题考查了y=Asin（ωx+φ）型函数的图象好性质，考查了三角函数的平移．三角函数的平移原则为左加右减上加下减，是中档题．
练习册系列答案
相关题目
已知函数f（x）=
，则f（f（4））的值为（ ）
|
A、-
| ||
B、
| ||
| C、-2 | ||
| D、2 |
（文科）若方程
-
=1表示焦点在x轴上的椭圆，则实数m的取值范围是（ ）
| x2 |
| m+2 |
| y2 |
| m-1 |
A、（-
| ||
B、（-
| ||
| C、（-∞，1） | ||
| D、（-2，1） |
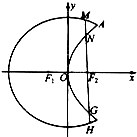我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”．如图，“盾圆C”是由椭圆