题目内容
10.计算:cos(2arccos$\frac{12}{13}$)=$\frac{119}{169}$.分析 设arccos$\frac{12}{13}$=α,则cosα=$\frac{12}{13}$,利用二倍角公式,可得结论.
解答 解:设arccos$\frac{12}{13}$=α,则cosα=$\frac{12}{13}$,
∴cos(2arccos$\frac{12}{13}$)=cos2α=2cos2α-1=$\frac{119}{169}$.
故答案为:$\frac{119}{169}$.
点评 本题考查二倍角的余弦公式,考查反三角函数知识的运用,比较基础.

练习册系列答案
相关题目
15.在(a+b)n中展开式中第7项二项式系数最大,则n=( )
| A. | 12 | B. | 11或13 | C. | 11或12或13 | D. | 12或13 |
2.在数列{an}中,a1=2,an+1=1-$\frac{1}{{a}_{n}}$,则a2010=( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
19.若框图所给的程序运行结果为S=1,那么判断框中应填入的关于k的条件可以是( )
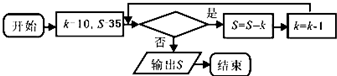

| A. | k=7 | B. | k≤6 | C. | k<6 | D. | k>6 |
20.已知实数x,y满足条件$\left\{\begin{array}{l}{1≤x+y≤3}\\{-1≤x-y≤1}\end{array}\right.$,那么2x+y的取值范围是( )
| A. | [0,6] | B. | [2,5] | C. | [2,4] | D. | [1,5] |