题目内容
1.甲、乙两位乒乓球选手,在过去的40局比赛中,甲胜24局.现在两人再次相遇.(1)打满3局比赛,甲最有可能胜乙几局,说明理由;
(2)采用“三局两胜”或“五局三胜”两种赛制,哪种对甲更有利,说明理由.(注:计算时,以频率作为概率的近似值.“三局两胜”就是有一方胜局达到两局时,就结束比赛;“五局三胜”就是有一方胜局达到三局时,就结束比赛)
分析 (1)由已知得甲胜k(k=0,1,2,3)局的概率为${P}_{3}(k)={C}_{3}^{k}{p}^{k}(1-p)^{3-k}$,由此能求出甲最有可能胜两局.
(2)分别求出三局两胜制甲胜的概率和五局三胜制甲胜的概率,由此能得到采用“五局三胜制”对甲有利.
解答 解:(1)比赛一局,甲胜的概率约为p=$\frac{24}{40}$=0.6.…(1分)
甲胜k(k=0,1,2,3)局的概率为${P}_{3}(k)={C}_{3}^{k}{p}^{k}(1-p)^{3-k}$.…(2分)
则${P}_{3}(0)={C}_{3}^{0}0.{4}^{3}$=0.0064,
${P}_{3}(1)={C}_{3}^{1}0.6•0.{4}^{2}$=0.288,
${p}_{3}(2)={C}_{3}^{2}0.{6}^{2}•0.4$=0.432,
${P}_{3}(3)={C}_{3}^{3}0.{6}^{3}$=0.216,…(5分)
因为甲P3(2)最大,所以甲最有可能胜两局.…(6分)
(2)三局两胜制:
甲胜的概率为P1=P2(2)+P2(1)×0.6=0.648,…(8分)
五局三胜制:
甲胜的概率为P2=P3(3)+P3(2)×0.6+P4(2)×0.6≈0.683,…(11分)
因为P2>P1,所以采用“五局三胜制”对甲有利.…(12分)
点评 本题考查概率的求法及应用,是中档题,解题时要认真审题,注意n次独立重复试验中事件A恰好发生k次的概率计算公式的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.求三个不相等的实数a,b,c最大值的程序框图如图所示,则空白判断框内应为( )
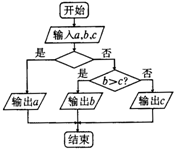

| A. | a>b? | B. | a>c? | C. | d>b或a>c? | D. | a>b且a>c? |
6.若数列{an}的前n项的和Sn=3an-2,则这个数列的通项公式为( )
| A. | ${a_n}={(\frac{3}{2})^{n-1}}$ | B. | ${a_n}=3×{(\frac{1}{2})^{n-1}}$ | C. | an=3n-2 | D. | ${a_n}={3^{n-1}}$ |