题目内容
20.已知实数x,y满足条件$\left\{\begin{array}{l}{1≤x+y≤3}\\{-1≤x-y≤1}\end{array}\right.$,那么2x+y的取值范围是( )| A. | [0,6] | B. | [2,5] | C. | [2,4] | D. | [1,5] |
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,即可求z的取值范围.
解答 解:作出不等式组对应的平面区域如图:(阴影部分).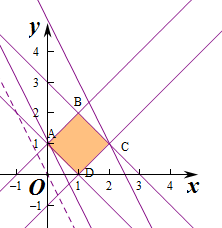
由z=2x+y得y=-2x+z,
平移直线y=-2x+z,
由图象可知当直线y=-2x+z经过点C时,直线y=-2x+z的截距最大,
此时z最大.
由$\left\{\begin{array}{l}{x+y=3}\\{x-y=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,即C(2,1),
代入目标函数z=2x+y得z=2×2+1=5.
当直线y=-2x+z经过点A时,直线y=-2x+z的截距最小,
此时z最小.
由$\left\{\begin{array}{l}{x+y=1}\\{x-y=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$,即A(0,1),
代入目标函数z=2x+y得z=2×0+1=1.
即目标函数z=2x+y的最小值为1.
目标函数z=2x+y的取值范围是[1,5].
故选:D.
点评 本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
相关题目
15.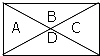 用5种不同的颜色给如图标有A,B,C,D的各部分涂色,每部分只涂一种颜色,且相邻两部分不同颜色,则不同的涂色方法共有( )
用5种不同的颜色给如图标有A,B,C,D的各部分涂色,每部分只涂一种颜色,且相邻两部分不同颜色,则不同的涂色方法共有( )
 用5种不同的颜色给如图标有A,B,C,D的各部分涂色,每部分只涂一种颜色,且相邻两部分不同颜色,则不同的涂色方法共有( )
用5种不同的颜色给如图标有A,B,C,D的各部分涂色,每部分只涂一种颜色,且相邻两部分不同颜色,则不同的涂色方法共有( )| A. | 160种 | B. | 240种 | C. | 260种 | D. | 360种 |
5.对某种灯泡中随机地抽取200个样品进行使用寿命调查,结果如下:
规定:使用寿命大于或等于500天的灯泡是优等品,小于300天是次品,其余的是正品.某人从灯泡样品中随机地购买了n(n∈N*)个,如果这n个灯泡的等级分布情况恰好与从这200个样品中按三个等级分层抽样所得的结果相同,则n的最小值为( )
| 寿命(天) | 频数 | 频率 |
| [100,200) | 20 | 0.10 |
| [200,300) | 30 | y |
| [300,400) | 70 | 0.35 |
| [400,500) | x | 0.15 |
| [500,600) | 50 | 0.25 |
| 合计 | 200 | 1 |
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
12.下列函数既是奇函数,又在区间[-1,1]上是单调递减的是( )
| A. | f(x)=x3 | B. | f(x)=-|x+1| | C. | f(x)=ln$\frac{2-x}{2+x}$ | D. | f(x)=$\frac{{a}^{x}+{a}^{-x}}{2}$ |