题目内容
5.已知抛物线y2=$\frac{1}{4}$x,直线l与该抛物线交于A,B两点(1)若线段AB的中点为(1,2),求直线l的方程
(2)若A,B两点到抛物线的F的距离之和为6,求直线l斜率的范围.
分析 (1)设直线AB方程的斜率为k,根据中点M的坐标写出直线AB的方程,把直线AB与抛物线方程联立,消去y得到关于x的一元二次方程,设出点A和B的坐标,根据韦达定理表示出两点的横坐标之和,然后再根据中点坐标公式,由线段AB的中点M的横坐标,列出关于k的方程,求出方程的解即可得到k的值,写出直线AB的方程即可.
(2)设直线l的方程为y=kx+b,代入抛物线方程,消去y,利用韦达定理、抛物线的定义,即可求直线l斜率的范围.
解答 解:(1)设直线AB的方程的斜率为k,则直线AB的方程为:y-2=k(x-1),
联立直线AB与抛物线方程,消去y得:k2x2-(2k2-4k+$\frac{1}{4}$)x+(-k+2)2=0,
设A(x1,y1),B(x2,y2),
则x1+x2=2-$\frac{4}{k}$+$\frac{1}{4{k}^{2}}$,
又线段AB的中点为M,
所以x1+x2=2,得到8k2-16k+1=8k2,解得k=$\frac{1}{16}$,
则直线AB的方程为:y-2=$\frac{1}{16}$(x-1)即x-16y+31=0.
(2)设直线l的方程为y=kx+b,代入抛物线方程,消去y得:k2x2+(2kb-$\frac{1}{4}$)x+b2=0,
所以x1+x2=-$\frac{2b}{k}$+$\frac{1}{4{k}^{2}}$,△>0,可得-kb+$\frac{1}{16}$>0①
因为A,B两点到抛物线的F的距离之和为6,
所以x1+x2+p=-$\frac{2b}{k}$+$\frac{1}{4{k}^{2}}$+$\frac{1}{8}$=6②
由①②可得k<-$\frac{\sqrt{47}}{47}$或k>$\frac{\sqrt{47}}{47}$.
点评 本题考查直线方程,考查直线与抛物线的位置关系,考查韦达定理的运用,属于中档题.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案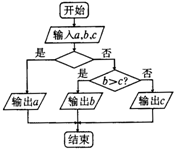
| A. | a>b? | B. | a>c? | C. | d>b或a>c? | D. | a>b且a>c? |
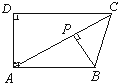 如图,已知四边形ABCD中AB∥CD,AD⊥AB,BP⊥AC,BP=PC,CD>AB,则经过某种翻折后以下线段可能会相互重合的是( )
如图,已知四边形ABCD中AB∥CD,AD⊥AB,BP⊥AC,BP=PC,CD>AB,则经过某种翻折后以下线段可能会相互重合的是( )| A. | AB与AD | B. | AB与BC | C. | BD与BC | D. | AD与AP |
| A. | 0 | B. | -1 | C. | -2 | D. | -3 |
| A. | 13 | B. | 53 | C. | 81 | D. | 161 |
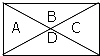 用5种不同的颜色给如图标有A,B,C,D的各部分涂色,每部分只涂一种颜色,且相邻两部分不同颜色,则不同的涂色方法共有( )
用5种不同的颜色给如图标有A,B,C,D的各部分涂色,每部分只涂一种颜色,且相邻两部分不同颜色,则不同的涂色方法共有( )| A. | 160种 | B. | 240种 | C. | 260种 | D. | 360种 |