题目内容
7.数列{an}的通项${a_n}=n({cos^2}\frac{nπ}{4}-{sin^2}\frac{nπ}{4})$,其前n项和为Sn,则S40为( )| A. | 10 | B. | 15 | C. | 20 | D. | 25 |
分析 ${a_n}=n({cos^2}\frac{nπ}{4}-{sin^2}\frac{nπ}{4})$=n$cos\frac{nπ}{2}$,可得:a2n-1=0,a2n=(-1)n•2n.即可得出.
解答 解:${a_n}=n({cos^2}\frac{nπ}{4}-{sin^2}\frac{nπ}{4})$=n$cos\frac{nπ}{2}$,
∴a1=0,a2=-2,a3=0,a4=4,a5=0,a6=-6,…,
可得a2n-1=0,a2n=(-1)n•2n.
则S40=(a1+a3+…+a39)+(a2+a4+…+a40)
=-2+4-…+40=20.
故选:C.
点评 本题考查了数列求和、分组求和、三角函数求值,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.已知向量$\overline{a}$,$\overline{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$=8,|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=4,则|2$\overrightarrow{a}$-$\overrightarrow{b}$|等于( )
| A. | 5 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 6 |
18.已知过点(-2,0)的直线与圆O:x2+y2-4x=0相切与点P(P在第一象限内),则过点P且与直线$\sqrt{3}$x-y=0垂直的直线l的方程为( )
| A. | x+$\sqrt{3}$y-2=0 | B. | x+$\sqrt{3}$y-4=0 | C. | $\sqrt{3}$x+y-2=0 | D. | x+$\sqrt{3}$y-6=0 |
19.已知m是直线,α,β是两个互相垂直的平面,则“m∥α”是“m⊥β”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
16.“墨子号”是由我国完全自主研制的世界上第一颗空间量子科学实验卫星,于2016年8月16日发射升空.“墨子号”的主要应用目标是通过卫星中转实现可覆盖全球的量子保密通信.量子通信是通过光子的偏振状态,使用二进制编码,比如,码元0对应光子偏振方向为水平或斜向下45度,码元1对应光子偏振方向为垂直或斜向上45度.如图所示
信号发出后,我们在接收端将随机选择两种编码方式中的一种来解码,比如,信号发送端如果按编码方式1发送,同时接收端按编码方式1进行解码,这时能够完美解码;信号发送端如果按编码方式1发送,同时接收端按编码方式2进行解码,这时无法获取信息.如果发送端发送一个码元,那么接收端能够完美解码的概率是$\frac{1}{2}$;如果发送端发送3个码元,那么恰有两个码元无法获取信息的概率是$\frac{3}{8}$.
| 编码方式1 | 编码方式2 | |
| 码元0 |  |  |
| 码元1 | 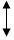 |  |
17.i是虚数单位,复数$\frac{2+{i}^{3}}{1-i}$=( )
| A. | $\frac{3+i}{2}$ | B. | $\frac{1+3i}{2}$ | C. | $\frac{1+i}{2}$ | D. | $\frac{3+2i}{2}$ |
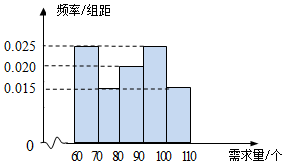 在某单位的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以x(单位:个,60≤x≤110)表示面包的需求量,T(单位:元)表示利润.
在某单位的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以x(单位:个,60≤x≤110)表示面包的需求量,T(单位:元)表示利润.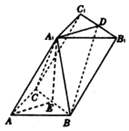 如图,在三棱柱ABC-A1B1C1中,D,E分别是B1C1、BC的中点,∠BAC=90°,AB=AC=2,A1A=4,A1E=$\sqrt{14}$.
如图,在三棱柱ABC-A1B1C1中,D,E分别是B1C1、BC的中点,∠BAC=90°,AB=AC=2,A1A=4,A1E=$\sqrt{14}$.