题目内容
(1)已知在等差数列{an}中,d=
,n=37,Sn=629,则求a1和an.
(2)已知在等比数列{bn}中,b1=-1,b4=64,求q和S4.
| 1 |
| 3 |
(2)已知在等比数列{bn}中,b1=-1,b4=64,求q和S4.
考点:等差数列的前n项和,等比数列的前n项和
专题:计算题,等差数列与等比数列
分析:(1)根据等差数列的通项公式与前n项和公式即可求出a1、an;
(2)根据等比数列的通项公式求出公比q和S4.
(2)根据等比数列的通项公式求出公比q和S4.
解答:
解:(1)∵等差数列{an}中,d=
,n=37,Sn=629,
∴
解得a1=11,
∴an=11+
(n-1)=
n+
;
(2)∵等比数列{bn}中,b1=-1,b4=64,
∴q3=-64,
解得q=-4;
∴S4=
=51.
| 1 |
| 3 |
∴
|
解得a1=11,
∴an=11+
| 1 |
| 3 |
| 1 |
| 3 |
| 32 |
| 3 |
(2)∵等比数列{bn}中,b1=-1,b4=64,
∴q3=-64,
解得q=-4;
∴S4=
| -1×(1-(-4)4) |
| 1-(-4) |
点评:本题考查了等差与等比数列的应用问题,解题时应灵活地应用等差与等比数列的公式进行计算,是基础题.

练习册系列答案
相关题目
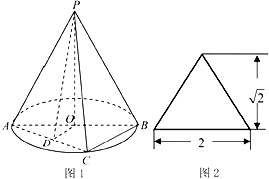 圆锥PO如图1所示,图2是它的正(主)视图.已知圆O的直径为AB,C是圆周上异于A、B的一点,D为AC的中点
圆锥PO如图1所示,图2是它的正(主)视图.已知圆O的直径为AB,C是圆周上异于A、B的一点,D为AC的中点 已知函数f(x)=2cos2(
已知函数f(x)=2cos2(