题目内容
7.已知圆C:x2+y2=5.(1)求直线y=x+2被圆C截得的弦长;
(2)求过点$N(\begin{array}{l}{1,}3\end{array})$的圆的切线方程.
分析 (1)求出圆心C到直线y=x+2的距离,利用勾股定理求直线y=x+2被圆C截得的弦长;
(2)设所求的切线方程为y-3=k(x-1),即kx-y+3-k=0,由$d=\sqrt{5}=\frac{{|{3-k}|}}{{\sqrt{{k^2}+1}}}$,整理得2k2+3k-2=0,求出k,即可求过点$N(\begin{array}{l}{1,}3\end{array})$的圆的切线方程.
解答 解:(1)圆心C(0,0),半径$r=\sqrt{5}$,…(2分)
圆心C到直线y=x+2的距离$d=\sqrt{2}$,弦长$|{AB}|=2\sqrt{5-2}=2\sqrt{3}$.…(4分)
(2)设所求的切线方程为y-3=k(x-1),即kx-y+3-k=0,
由$d=\sqrt{5}=\frac{{|{3-k}|}}{{\sqrt{{k^2}+1}}}$,整理得2k2+3k-2=0,解得k1=-2,${k_2}=\frac{1}{2}$,
两条直线方程为2x+y-5=0,x-2y+5=0. …(8分)
点评 本题考查直线与圆的位置关系,考查点到直线的距离公式,属于中档题.

练习册系列答案
相关题目
15.四棱柱ABCD-A1B1C1D1的三视图如图所示,则异面直线D1C与AC1所成的角为( )
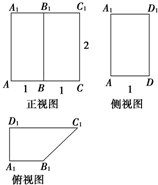

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
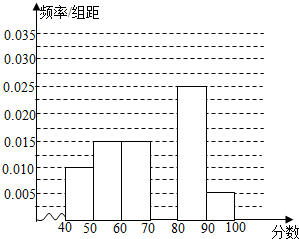 某校参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
某校参加高一年级期中考试的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60),…,[90,100)后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: