题目内容
12.设函数f(x)=$\frac{1}{3}{x}^{3}$-x2+m在[-1,1]上的最大值为$\frac{2}{3}$.(1)求实数m的值;
(2)求函数f(x)在[-2,2]上的值域.
分析 (1)求出f′(x)=x(x-2),当x∈(-1,0)时,f′(x)>0;当x∈(0,1)时,f′(x)<0,由此能求出m.
(2)由函数f(x)=$\frac{1}{3}{x}^{3}$-x2+$\frac{2}{3}$,f′(x)=x(x-2),利用导数性质能求出函数f(x)在[-2,2]上的值域.
解答 解:(1)∵函数f(x)=$\frac{1}{3}{x}^{3}$-x2+m,
∴f′(x)=x(x-2),
当x∈(-1,0)时,f′(x)>0;当x∈(0,1)时,f′(x)<0,
∵函数f(x)=$\frac{1}{3}{x}^{3}$-x2+m在[-1,1]上的最大值为$\frac{2}{3}$,
∴f(0)=m=$\frac{2}{3}$.
(2)由(1)得函数f(x)=$\frac{1}{3}{x}^{3}$-x2+$\frac{2}{3}$,
∴f′(x)=x(x-2),
由f′(x)=0,得x1=0,x2=2,
∵f(-2)=-6,f(0)=$\frac{2}{3}$,f(2)=-$\frac{2}{3}$,
∴函数f(x)在[-2,2]上的值域为[-6,$\frac{2}{3}$].
点评 本题考查实数值的求法,考查函数在闭区间上的值域的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
相关题目
3.定义在R上的函数f(x)满足f′(x)<1,f(1)=2,则满足f(2x-1)<2x的x的范围是( )
| A. | (1,+∞) | B. | (-∞,1) | C. | (-1,1) | D. | (-∞,1)∪(1,+∞) |
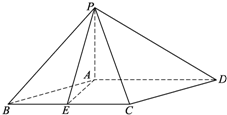 已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.
已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=2PA,E是线段BC的中点.