��Ŀ����
19����֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0���ϵ�һ����P�����ҽ���F1��F2�ľ���֮��Ϊ2$\sqrt{2}$����P����Բһ���������Զ����Ϊ$\sqrt{2}$+1��������Բ�ķ��̣�
�����ҽ���F2��ֱ�߽���Բ��A��B����
����y�����Ƿ����һ��M��0��$\frac{1}{3}$������|MA|=|MB|����ֱ��lб��k��ֵ��
���Ƿ����������ֱ��l��ʹS��ABO�����ֵΪ$\frac{\sqrt{2}}{2}$������OΪ����ԭ�㣩�������ڣ���ֱ��l�ķ��̣��������ڣ�˵�����ɣ�
���� ��I����Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0���Ľ�����x���ϣ�������Բ�����ʿ�֪��2a=2$\sqrt{2}$��a=$\sqrt{2}$��b2=a2-c2=1�����������Բ���̣�
��II����ֱ��l�ķ���Ϊ��y=k��x-1����������Բ���̣���x1+x2=$\frac{4{k}^{2}}{1+2{k}^{2}}$��x1•x2=$\frac{2{k}^{2}-2}{1+2{k}^{2}}$�����ҳ���ʽ��֪$\sqrt{1+{k}^{2}}$حx1-x2ح=$\sqrt{1+{k}^{2}}$$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$\frac{2\sqrt{2}��1+{k}^{2}��}{1+2{k}^{2}}$��
����ֱ�߷��̣��������õ��е����꣬����|MA|=|MB|���õ�MG���ڵ�ֱ����ֱ��l��ֱ��������ֱ��б��֮��Ϊ-1���������ֱ��lб��k��ֵ��
�ڷֳ�б�ʴ��ںͲ���������������ۣ��ֱ�����ҳ�حABح��ԭ�㵽ֱ�ߵľ��룬�����������ı���ʽ�����ݲ���ʽ���ɵõ������
��� �⣺��I����Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0���Ľ�����x���ϣ���P�����ҽ���F1��F2�ľ���֮��Ϊ2$\sqrt{2}$��
������Բ�����ʿ�֪��2a=2$\sqrt{2}$��a=$\sqrt{2}$����1��
��P����Բһ���������Զ����Ϊa+c=$\sqrt{2}$+1
��c=1��
b2=a2-c2=1����2��
����Բ�ı�����Ϊ��$\frac{{x}^{2}}{2}+{y}^{2}=1$����3��
��II���ɣ���֪��F2��1��0������ֱ��l�ķ���Ϊ��y=k��x-1����A ��x1��y1����B ��x2��y2����
����ֱ������Բ���̵ã�$\left\{\begin{array}{l}{y=k��x-1��}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$�������ã���1+2k2��x2-4k2x+2k2-2=0��
��x1+x2=$\frac{4{k}^{2}}{1+2{k}^{2}}$��x1•x2=$\frac{2{k}^{2}-2}{1+2{k}^{2}}$��
��y1+y2=k��x1+x2��-2k=-$\frac{2k}{1+2{k}^{2}}$��
حx1-x2ح=$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$=$\frac{2\sqrt{2}\sqrt{1+{k}^{2}}}{1+2{k}^{2}}$����4��
����AB���е�����ΪG��$\frac{2{k}^{2}}{1+2{k}^{2}}$��-$\frac{k}{1+2{k}^{2}}$������5��
��k��1ʱ����|MA|=|MB|���õ�MG���ڵ�ֱ����ֱ��l��ֱ��
��MG���ڵ�ֱ��б��Ϊ$\frac{-\frac{k}{1+2{k}^{2}}-\frac{1}{3}}{\frac{2{k}^{2}}{1+2{k}^{2}}-0}$=$\frac{-2k-1-2{k}^{2}}{6{k}^{2}}$=-$\frac{1}{k}$����ã�k=1��k=$\frac{1}{2}$����7��
��k=0ʱ��AB���д������ڵ�ֱ�ߵķ���Ϊx=0���������⣬
����������б��k��ȡֵΪ0��$\frac{1}{2}$��1����8��
��2����ֱ��l��б�ʲ�����ʱ����ʱA��1��$\frac{\sqrt{2}}{2}$����B��1��-$\frac{\sqrt{2}}{2}$�����õ�حABح=$\sqrt{2}$��
��S��ABO=$\frac{1}{2}$��1��$\sqrt{2}$=$\frac{\sqrt{2}}{2}$����9��
��ֱ��l��б�ʴ���ʱ��حABح=$\sqrt{1+{k}^{2}}$•حx1-x2ح=$\frac{2\sqrt{2}��1+{k}^{2}��}{1+2{k}^{2}}$����10��
ԭ�㵽ֱ��l�ľ���Ϊd=$\frac{حkح}{\sqrt{1+{k}^{2}}}$����11��
��S��ABO=$\frac{1}{2}$•حABح•d=$\sqrt{2}$حABح•d=$\sqrt{2}$$\sqrt{\frac{1}{4}-\frac{1}{4��1+2{k}^{2}��^{2}}}$����12��
��$\frac{1}{4��1+2{k}^{2}��^{2}}$��0��
����S��ABO��$\frac{\sqrt{2}}{2}$��
����������S��ABO�����ֵΪ$\frac{\sqrt{2}}{2}$
�������������ֱ�ߴ��ڣ�����Ϊx=1��14��
���� ���⿼����Բ�ı����̣�����ֱ������Բ��λ�ù�ϵ�������ҳ���ʽ��Τ�ﶨ�����㵽ֱ�ߵľ��빫ʽ�����������������ʽ���ۺ�Ӧ�ã�������Բ�벻��ʽ���ۺ�Ӧ�ã�������������������е��⣮

 ������״Ԫ���Ծ�ϵ�д�
������״Ԫ���Ծ�ϵ�д�| A�� | m��0 | B�� | m��-1 | C�� | m��2 | D�� | m��-$\frac{3}{2}$ |
| A�� | ֱ�������� | B�� | �ȱ������� | C�� | ���������� | D�� | ����ֱ�������� |
��1�������������ϻ�����ѧ�ɼ��������ɼ�����������
��2���ܷ��ڷ�����ĸ��ʲ�����0.050��ǰ������Ϊ��ѧ�ɼ��������ɼ��й�ϵ��
�ο���ʽ��K2=$\frac{n��ad-bc��^{2}}{��a+b����c+d����a+c����b+d��}$��n=a+b+c+d
| P��K2��k0�� | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |

| A�� | $\frac{24��}{3}$ | B�� | $\frac{4��}{3}$ | C�� | $\frac{2��}{3}$ | D�� | $\frac{��}{3}$ |
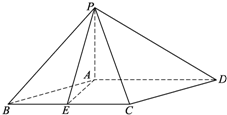 ��֪����P-ABCD�У�PA��ƽ��ABCD������ABCDΪ���Σ���ABC=60�㣬AB=2PA��E���߶�BC���е㣮
��֪����P-ABCD�У�PA��ƽ��ABCD������ABCDΪ���Σ���ABC=60�㣬AB=2PA��E���߶�BC���е㣮