题目内容
17．设双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的左、右焦点分别为F1，F2，过F2的直线与双曲线的右支交于两点A，B，若|AF1|：|AB|=3：4，且F2是AB的一个四等分点，则双曲线C的离心率是（ ）| A． | $\frac{{\sqrt{5}}}{2}$ | B． | $\frac{{\sqrt{10}}}{2}$ | C． | $\frac{5}{2}$ | D． | 5 |
分析 根据双曲线的定义得到三角形F1AB是直角三角形，根据勾股定理建立方程关系即可得到结论．
解答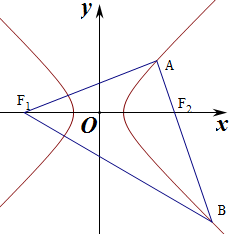 
解：设|AB|=4x，则|AF1|=3x，|AF2|=x，
∵|AF1|-|AF2|=2a，∴x=a，
∴|AB|=4a，|BF1|=5a，
∴满足|AF1|2+|AB|2=|BF1|2，
则∠F1AB=90°，
则|AF1|2+|AF2|2=|F1F2|2，
即9a2+a2=4c2，
即10a2=4c2，
得e=$\frac{c}{a}$=$\frac{\sqrt{10}}{2}$，
故选B．
点评 本题主要考查双曲线离心率的求解，根据条件结合双曲线的定义判断三角形F1AB是直角三角形是解决本题的关键．
练习册系列答案
相关题目
7．
某三棱锥的三视图如图所示，其中三个视图都是直角三角形，则该三棱锥外接球的体积为（ ）
某三棱锥的三视图如图所示，其中三个视图都是直角三角形，则该三棱锥外接球的体积为（ ）| A． | 2π | B． | $\sqrt{6}π$ | C． | 6π | D． | $4\sqrt{3}π$ |
5．若实数x，y，满足2x-y-5=0，则$\sqrt{{x^2}+{y^2}}$的最小值是（ ）
| A． | $\frac{{\sqrt{5}}}{5}$ | B． | 1 | C． | $\sqrt{5}$ | D． | 5 |
12．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的左、右焦点分别为F1、F2，焦距为2c（c＞0），抛物线y2=2cx的准线交双曲线左支于A，B两点，且∠AOB=120°（O为坐标原点），则该双曲线的离心率为（ ）
| A． | $\sqrt{3}+1$ | B． | 2 | C． | $\sqrt{2}+1$ | D． | $\sqrt{5}+1$ |
2．统计某产品的广告费用x与销售额y的一组数据如表：
若根据如表提供的数据用最小二乘法可求得y对x的回归直线方程是$\stackrel{∧}{y}$=1.1x+4.6，则数据中的m的值应该是8．
| 广告费用x | 2 | 3 | 5 | 6 |
| 销售额y | 7 | m | 9 | 12 |
9．已知的取值如表所示：
如果y与x线性相关，且线性回归方程$y=bx+\frac{13}{2}$，则$\stackrel{∧}{b}$=（ ）
| x | 2 | 3 | 4 |
| y | 6 | 4 | 5 |
| A． | $-\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{1}{4}$ | D． | $-\frac{5}{6}$ |
6．函数f（x）=sin（ωx+φ）（ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）在区间（$\frac{π}{4}$，$\frac{π}{2}$）内是增函数，则（ ）
| A． | f（$\frac{π}{4}$）=-1 | B． | f（x）的周期为$\frac{π}{2}$ | C． | ω的最大值为4 | D． | f（$\frac{3π}{4}$）=0 |
7．若实数x，y满足$\left\{\begin{array}{l}{2x-y+2≥0}\\{2x+y-6≤0}\\{0≤y≤3}\end{array}\right.$，且z=mx-y（m＜2）的最小值为-$\frac{5}{2}$，则m等于（ ）
| A． | $\frac{5}{4}$ | B． | -$\frac{5}{6}$ | C． | 1 | D． | $\frac{1}{3}$ |