题目内容
10.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+m(m为常数),则f(-1)=( )| A. | 3 | B. | 1 | C. | -1 | D. | -3 |
分析 由奇函数的性质可得f(0)=0可求m,从而可求x≥0时的函数的解析式,再由f(-1)=-f(1)可求.
解答 解:由函数为奇函数可得f(0)=1+m=0,
∴m=-1,
∵x≥0时,f(x)=2x-1,
∴f(-1)=-f(1)=-1.
故选C.
点评 本题主要考查了奇函数的定义f(-x)=-f(x)在函数求值中的应用,解题的关键是利用f(0)=0求出m.

练习册系列答案
相关题目
20.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,O为坐标原点,点P是双曲线在第一象限内的点,直线PO,PF2分别交双曲线C的左、右支于另一点M,N,若|PF1|=2|PF2|,且∠MF2N=120°,则双曲线的离心率为( )
| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\sqrt{7}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
18.用数学归纳法证明不等式“$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}>\frac{13}{24}(n>2)$”时的过程中,由n=k到n=k+1,(k>2)时,不等式的左边( )
| A. | 增加了一项$\frac{1}{2(k+1)}$ | |
| B. | 增加了两项$\frac{1}{2k+1}+\frac{1}{2(k+1)}$ | |
| C. | 增加了一项$\frac{1}{2(k+1)}$,又减少了一项$\frac{1}{k+1}$ | |
| D. | 增加了两项$\frac{1}{2k+1}+\frac{1}{2(k+1)}$,又减少了一项$\frac{1}{k+1}$ |
5.若实数x,y,满足2x-y-5=0,则$\sqrt{{x^2}+{y^2}}$的最小值是( )
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | 1 | C. | $\sqrt{5}$ | D. | 5 |
2.统计某产品的广告费用x与销售额y的一组数据如表:
若根据如表提供的数据用最小二乘法可求得y对x的回归直线方程是$\stackrel{∧}{y}$=1.1x+4.6,则数据中的m的值应该是8.
| 广告费用x | 2 | 3 | 5 | 6 |
| 销售额y | 7 | m | 9 | 12 |
20.若函数f(x)=sin(2x+$\frac{π}{6}$)+cos(2x-$\frac{π}{3}$),则f(x)的单调递增区间为( )
| A. | (kπ-$\frac{7π}{12}$,kπ-$\frac{π}{12}$),k∈Z | B. | (kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$),k∈Z | ||
| C. | (kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$),k∈Z | D. | (kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$),k∈Z |
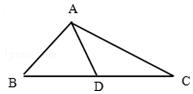 如图,在△ABC中,BC边上的中线AD长为3,且BD=2,sinB=$\frac{3\sqrt{6}}{8}$.
如图,在△ABC中,BC边上的中线AD长为3,且BD=2,sinB=$\frac{3\sqrt{6}}{8}$.