题目内容
3．设角α的终边过点P（-4t，3t）（t∈R，且t＞0），则2sinα+cosα=$\frac{2}{5}$．分析 由条件利用任意角的三角函数的定义，求得要求式子的值．
解答 解：∵角α的终边过点P（-4t，3t）（t∈R，且t＞0），
∴r=|OP|=5t，x=-4t，y=3t，∴sinα=$\frac{y}{r}$=$\frac{3}{5}$，cosα=$\frac{x}{r}$=-$\frac{4}{5}$，
则2sinα+cosα=$\frac{6}{5}$-$\frac{4}{5}$=$\frac{2}{5}$，
故答案为：$\frac{2}{5}$．
点评 本题主要考查任意角的三角函数的定义，属于基础题．
练习册系列答案
相关题目
14．已知集合A={x|1＜x+2＜5}，B={x|-1＜x＜1}，则（ ）
| A． | A?B | B． | B?A | C． | A=B | D． | A∩B=∅ |
11．已知α是第一象限角，sinα-cosα=$\frac{{\sqrt{5}}}{5}$，则cos2α=（ ）
| A． | $-\frac{3}{5}$ | B． | $±\frac{3}{5}$ | C． | $\frac{4}{5}$ | D． | $±\frac{4}{5}$ |
18．
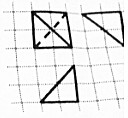如图，网格纸上正方形小格的边长为1（表示1cm），图中粗线画出的是一个四面体的三视图，则该四面体外接球的体积与四面体的体积的比值为（ ）
如图，网格纸上正方形小格的边长为1（表示1cm），图中粗线画出的是一个四面体的三视图，则该四面体外接球的体积与四面体的体积的比值为（ ）| A． | 2$\sqrt{2}$π | B． | 3$\sqrt{3}$π | C． | 4π | D． | 2$\sqrt{5}$π |
8．已知函数f（x）满足条件：当x＞0时，f（x）+$\frac{1}{2}$xf′（x）＞1，则下列不等式正确的是（ ）
| A． | f（1）+3≥4f（2） | B． | f（1）+3＞4f（2） | C． | f（1）+3＜4f（2） | D． | f（2）+3＞4f（4） |