题目内容

18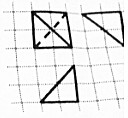．如图，网格纸上正方形小格的边长为1（表示1cm），图中粗线画出的是一个四面体的三视图，则该四面体外接球的体积与四面体的体积的比值为（　　）
A．2$\sqrt{2}$πB．3$\sqrt{3}$πC．4πD．2$\sqrt{5}$π

分析 根据几何体的三视图，得出该几何体是由正方体截割得到的三棱锥，画出图形结合图形求出对应的体积，由此计算所求的体积比值．

解答 解：根据几何体的三视图，得：
该几何体是由正方体截割得到，如图中三棱锥A-BCD，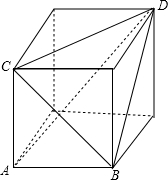

由三视图中的网络纸上小正方形边长为1，
得该正方体的棱长为2，
所以该三棱锥的体积为V三棱锥=$\frac{1}{3}$×$\frac{1}{2}$×22×2=$\frac{4}{3}$，
则该四面体外接球的体积为V外接球=$\frac{4π}{3}$•${（\frac{2\sqrt{3}}{2}）}^{3}$=$\frac{4π}{3}$•3$\sqrt{3}$；
故所求的体积比值为3$\sqrt{3}$π．
故选：B．

点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．

练习册系列答案
相关题目
8．已知|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2，对任意x∈R，若不等式|$\overrightarrow{a}$+x$\overrightarrow{b}$|≥1恒成立，则$\overrightarrow{a}$•$\overrightarrow{b}$的取值范围是$[{-2\sqrt{3}，2\sqrt{3}}]$．
9．已知函数f（x）=x2+alnx
（1）当a=-8时，求函数的单调区间；
（2）若函数g（x）=f（x）+$\frac{2}{x}$在[2，+∞）上是单调递增函数，求实数a的取值范围．
6．函数f（x）=-x2+2ax与g（x）=$\frac{1-ax}{x+1}$在区间（1，2）上都单调递减，则实数a的取值范围是（-1，1]．
13．化简$\frac{3cos（\frac{π}{2}+α）-cos（π-α）}{sin（α-\frac{π}{2}）-3sin（π+α）}$=-1，tan25°+tan35°+$\sqrt{3}$tan25°tan35°=$\sqrt{3}$．
3．设角α的终边过点P（-4t，3t）（t∈R，且t＞0），则2sinα+cosα=$\frac{2}{5}$．
10．下面给出的四个命题中：
①以抛物线y2=4x的焦点为圆心，且过坐标原点的圆的方程为（x-2）2+y2=4；
②若m=-2，则直线（m+2）x+my+1=0与直线（m-2）x+（m+2）y-3=0相互垂直；
③命题“?x∈R，使得x2+3x+4=0”的否定是“?x∈R，都有x2+3x+4≠0”；
④将函数y=sin2x的图象向右平移$\frac{π}{3}$个单位，得到函数y=sin（2x-$\frac{π}{3}$）的图象．
其中是真命题的有②③（将你认为正确命题的序号都填上）．
7．已知数列{an}满足an+1=$\frac{2{a}_{n}}{{a}_{n}+2}$，a1=1，n∈N*．
（1）求a2，a3，a4的值；
（2）求数列{an}的通项公式．
8．等差数列{an}中，若a5=7，则（　　）
A．S9=63B．S11=63C．S9=35D．S11=77

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网