题目内容
16．已知函数f（x）=ax2+bx+c的图象关于y轴对称，则f（x）=kx+b的图象关于原点对称．分析 根据偶函数关于y轴对称，奇函数关于原点对称判断即可．
解答 解：f（x）=ax2+bx+c的图象关于y轴对称，
∴函数为偶函数，
∴b=0，
∴f（x）=kx+b=kx，为奇函数，
∴图象关于原点对称．
故答案为：原点．
点评 考查了函数的奇偶性，属于基础题型，应熟练掌握．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
4．已知命题p：?x∈R，x2-x-2≥0，那么命题?p为（ ）
| A． | ?x∈R，x2-x-2≤0 | B． | ?x∈R，x2-x-2＜0 | C． | ?x∈R，x2-x-2≤0 | D． | ?x∈R，x2-x-2＜0 |
11．已知集合A={1，2}，B={2，3，4}，那么集合A∩B等于（ ）
| A． | {2} | B． | {2，3} | C． | {1，2，3} | D． | {1，2，3，4} |
8．
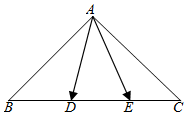如图，在等腰直角三角形ABC中，AB=AC=$\sqrt{2}$，D，E是线段BC上的点，且DE=$\frac{1}{3}$BC，则$\overrightarrow{AD}$•$\overrightarrow{AE}$的取值范围是（ ）
如图，在等腰直角三角形ABC中，AB=AC=$\sqrt{2}$，D，E是线段BC上的点，且DE=$\frac{1}{3}$BC，则$\overrightarrow{AD}$•$\overrightarrow{AE}$的取值范围是（ ）| A． | $[{\frac{8}{9}，\;\frac{4}{3}}]$ | B． | $[{\frac{4}{3}，\;\frac{8}{3}}]$ | C． | $[{\frac{8}{9}，\;\frac{8}{3}}]$ | D． | $[{\frac{4}{3}，\;+∞}）$ |
5．
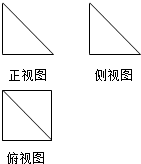一个几何体的三视图如图所示，其中正视图和俯视图的都是腰长为1的两个全等的等腰直角三角形，则该几何体的体积为（ ）
一个几何体的三视图如图所示，其中正视图和俯视图的都是腰长为1的两个全等的等腰直角三角形，则该几何体的体积为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{6}$ |