题目内容

6．已知函数f（x）=$\left\{\begin{array}{l}{（\frac{1}{10}）^{x}，x≤10}\\{-lg（x+2），x＞10}\end{array}\right.$，若f（8-m2）＜f（2m），则实数m的取值范围是（-4，2）．

分析 先求出函数的单调性，根据函数单调性的性质得到关于m的不等式，解出即可．

解答 解：∵函数f（x）=$\left\{\begin{array}{l}{（\frac{1}{10}）^{x}，x≤10}\\{-lg（x+2），x＞10}\end{array}\right.$，
∴函数f（x）在R上单调递减，
由f（8-m2）＜f（2m），
得：8-m2＞2m，解得：-4＜m＜2，
故答案为：（-4，2）．

点评 本题考查了函数的单调性的应用，考查指数函数、对数函数的性质，是一道中档题．

练习册系列答案
相关题目
6．已知A，B两地间的距离为20km，B，C两地间的距离为40km，现测得∠ABC=120°，则A，C两地间的距离为（　　）
A．20kmB．20$\sqrt{3}$kmC．20$\sqrt{5}$kmD．20$\sqrt{7}$km
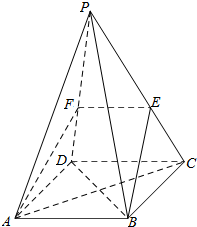17．如图，在四棱锥P-ABCD中，底面ABCD是菱形，PB=PD，过AB的平面分别交棱PC，PD于点E，F．
（Ⅰ）求证：EF∥AB；
（Ⅱ）求证：BD⊥平面PAC．
14．求椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的顶点坐标、焦点坐标、长轴长、短轴长、焦距和离心率．
1．设θ为第二象限角，若$tan（θ+\frac{π}{4}）=\frac{1}{2}$．求
（Ⅰ）tanθ的值；
（Ⅱ）$sin（\frac{π}{2}-2θ）+sin（π+2θ）$的值．
11．已知椭圆$\frac{x^2}{k+6}$+$\frac{y^2}{k}$=1的上顶点为A、右顶点为B，直线x-2y=0过线段AB的中点，则实数k等于（　　）
A．2B．3C．4D．6
18．已知函数f（x）是奇函数，当x∈（-∞，0）时，f（x）=$\frac{x}{1-x}$．
（1）求f（1）的值；
（2）求函数f（x）在（0，+∞）上的解析式；
（3）判断函数f（x）在（0，+∞）上的单调性，并用单调性的定义证明你的结论．
15．设函数f（x）=x+ax2+blnx，曲线y=f（x）过点P（1，0），且在P点处的切线斜率为2．
（1）求a，b的值；
（2）设函数g（x）=f（x）-2x+2，证明：g（x）≤0．
16．已知函数f（x）=ax2+bx+c的图象关于y轴对称，则f（x）=kx+b的图象关于原点对称．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网