题目内容
11.设x、y∈R,复数z=(|x|-y)+(x-2y+2)i表示的点在第二象限,则x+y的取值范围为(0,4).分析 根据复数z表示的点在第二象限,得出不等式组$\left\{\begin{array}{l}{|x|-y<0}\\{x-2y+2>0}\end{array}\right.$,画出它表示的平面区域,求出最优解即可得出x+y的取值范围.
解答 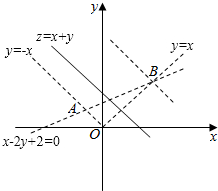 解:复数z=(|x|-y)+(x-2y+2)i表示的点在第二象限,
解:复数z=(|x|-y)+(x-2y+2)i表示的点在第二象限,
∴$\left\{\begin{array}{l}{|x|-y<0}\\{x-2y+2>0}\end{array}\right.$,
画出该不等式组表示的平面区域,是△OAB的内部,不包括边界,
如图所示;
∴当点在边界OA上时,即y=-x,x+y=0;
当点在B(2,2)处时,x+y=4;
∴x+y的取值范围是(0,4).
故答案为:(0,4).
点评 本题考查了复数的概念与应用问题,也考查了线性规划的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目